使用Pandas和Matplotlib绘制Lex等人提出的UpSet图
项目描述
这是Lex等人UpSet图的另一种Python实现。[Lex2014]。UpSet图用于可视化集合重叠;类似于维恩图,但更易于阅读。文档在https://upsetplot.readthedocs.io。
这个upsetplot库试图提供一个简单的接口,背后是可扩展的、面向对象的设计。
数据分类有许多表示方法,如我们数据格式指南所述。
我们的内部输入格式使用包含对应于子集大小的计数的
>>> from upsetplot import generate_counts
>>> example = generate_counts()
>>> example
cat0 cat1 cat2
False False False 56
True 283
True False 1279
True 5882
True False False 24
True 90
True False 429
True 1957
Name: value, dtype: int64
然后
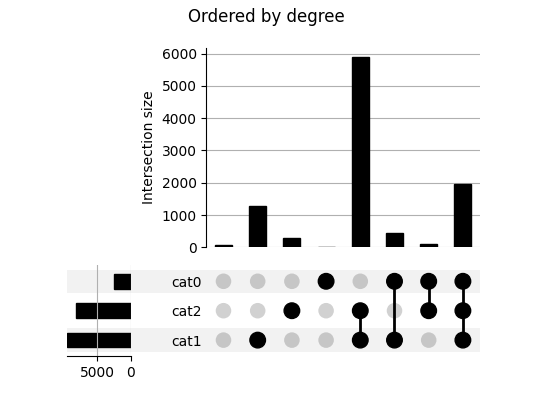
>>> from upsetplot import plot >>> plot(example) # doctest: +SKIP >>> from matplotlib import pyplot >>> pyplot.show() # doctest: +SKIP
使得
您可以将图像保存为各种格式
>>> pyplot.savefig("/path/to/myplot.pdf") # doctest: +SKIP
>>> pyplot.savefig("/path/to/myplot.png") # doctest: +SKIP
此图显示了在我们数据中看到的所有类别组合的基数。最左侧的列计算任何类别中缺失的项目。接下来的三列分别计算仅存在于cat1、cat2和cat3中的项目。接下来的几列显示每个恰好两个命名集合的组合中的项目的基数。最右侧的列计算所有三个集合中的项目。
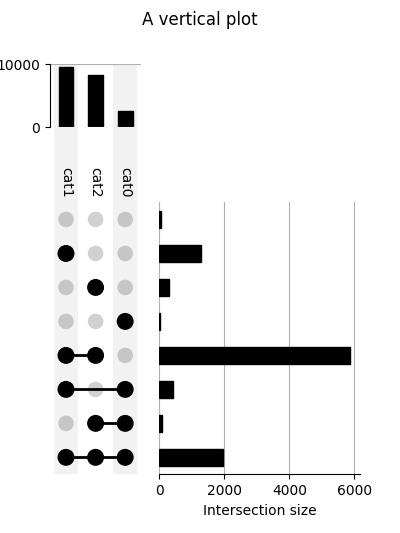
旋转
我们称上述绘图样式为“水平”,因为类别交集是从左到右呈现的。垂直图也支持!
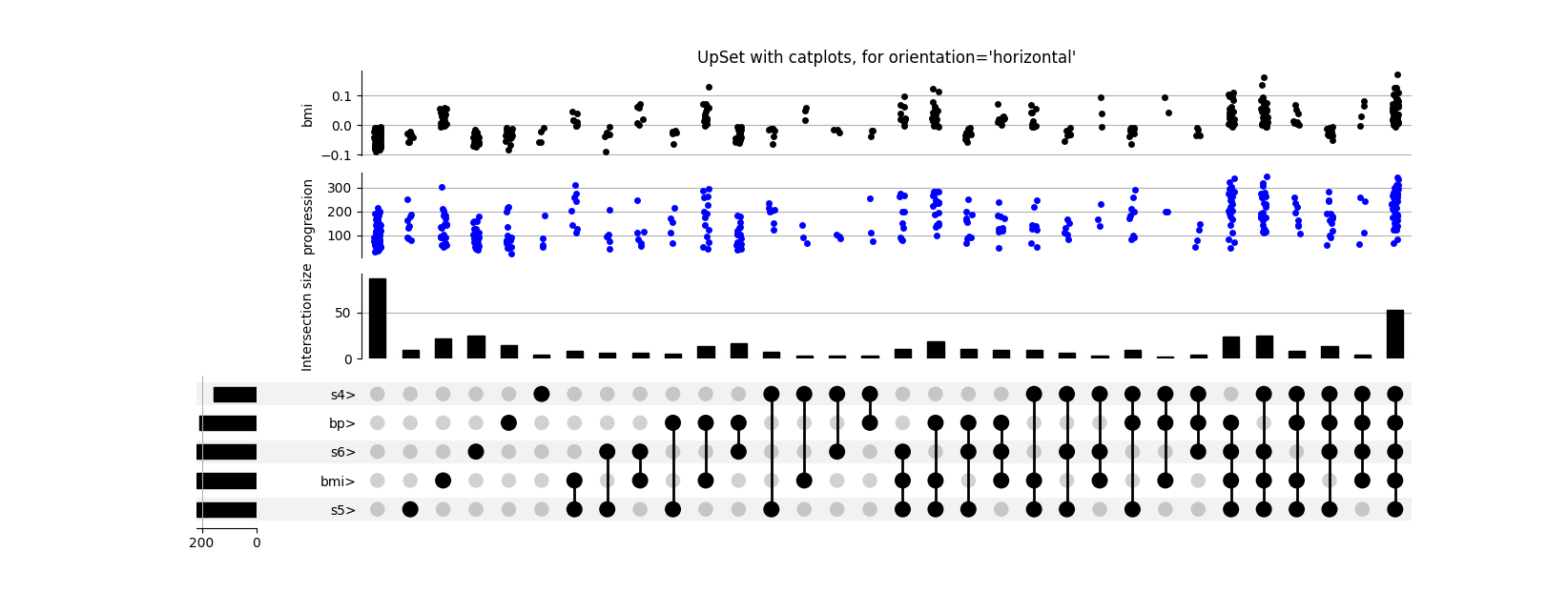
分布
使用DataFrame而不是Series作为输入,可以使我们更直观地绘制每个子集变量的分布。
加载数据集
虽然上述数据集是随机生成的,但你也可以为upsetplot准备自己的数据集。一个有用的工具是from_memberships,它允许我们通过指示每个数据点的类别成员资格来重建上述示例。
>>> from upsetplot import from_memberships
>>> example = from_memberships(
... [[],
... ['cat2'],
... ['cat1'],
... ['cat1', 'cat2'],
... ['cat0'],
... ['cat0', 'cat2'],
... ['cat0', 'cat1'],
... ['cat0', 'cat1', 'cat2'],
... ],
... data=[56, 283, 1279, 5882, 24, 90, 429, 1957]
... )
>>> example
cat0 cat1 cat2
False False False 56
True 283
True False 1279
True 5882
True False False 24
True 90
True False 429
True 1957
dtype: int64
还可以参考from_contents,另一种描述分类数据的方式,以及from_indicators,它允许通过数据框(或列数据的函数,如是否存在缺失值)中的列来指示每个类别。
安装
要安装库,您可以使用pip
$ pip install upsetplot
安装需要
pandas
matplotlib >= 2.0
seaborn 以使用 UpSet.add_catplot
然后应该可以在Python中
>>> import upsetplot
。
为什么是py-upset的替代品?
可能是因为一些微不足道的原因。py-upset似乎没有维护。其输入格式未经文档记录,效率低下,我认为不合适。它不支持Python 2。我决定构建一个更干净的版本,而不是修复它。
参考文献
Alexander Lex,Nils Gehlenborg,Hendrik Strobelt,Romain Vuillemot,Hanspeter Pfister,UpSet: Visualization of Intersecting Sets,IEEE Transactions on Visualization and Computer Graphics (InfoVis ‘14),vol. 20,no. 12,pp. 1983–1992,2014。doi: doi.org/10.1109/TVCG.2014.2346248










