Shenfun -- 自动化谱伽辽金框架
项目描述





描述
Shenfun是一个高性能计算平台,通过谱伽辽金方法求解偏微分方程(PDEs)。Shenfun的用户界面与FEniCS非常相似,但应用限于多维张量积网格,使用笛卡尔或曲线网格(例如,但不仅限于,极坐标、圆柱坐标、球坐标或抛物线坐标)。代码通过mpi4py-fft包使用MPI进行并行化。
Shenfun使用高级Python语言,使得高效且准确的PDE求解器(谱阶和精度)的开发变得快速。通过使用高阶全局正交基函数(傅里叶、勒让德、切比雪夫第一和第二类、超球面、雅可比、拉盖尔和厄米特),保证了谱精度,与使用低阶局部基函数的有限元代码相反。通过向量化(Numpy)、并行化(mpi4py)以及将关键例程移至Cython或Numba,保证了效率。Shenfun已被用于在高性能超级计算机上运行数千个处理器的湍流模拟(直接数值模拟),请参阅spectralDNS存储库。
示例文件夹包含了泊松、亥姆霍兹和双调和方程的几个示例。有关扩展文档和安装说明,请参阅ReadTheDocs。有关交互式演示,请参阅jupyter book。请注意,shenfun当前支持使用两个非周期方向(见双调和演示),方程可以耦合和隐式求解(见MixedPoisson.py)。
请注意,shenfun支持曲线坐标。例如,可以在球体(使用球坐标)上求解方程,在环面上,在莫比乌斯带上,或在2D/3D中的任何曲线线上。实际上,只要坐标导致具有可分离系数的方程组,用户就可以定义任何新的坐标。在定义新的坐标后,div、grad和curl等算子会自动与新的曲线坐标一起工作。请参阅关于球体的这个笔记本或向量拉普拉斯的插图。
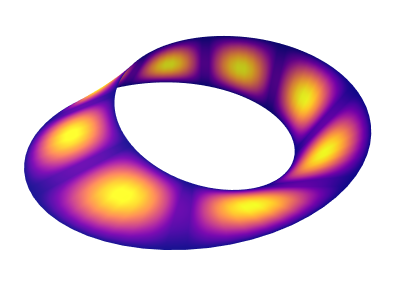
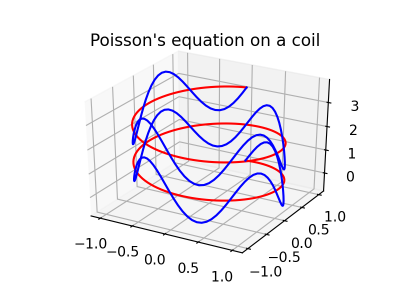
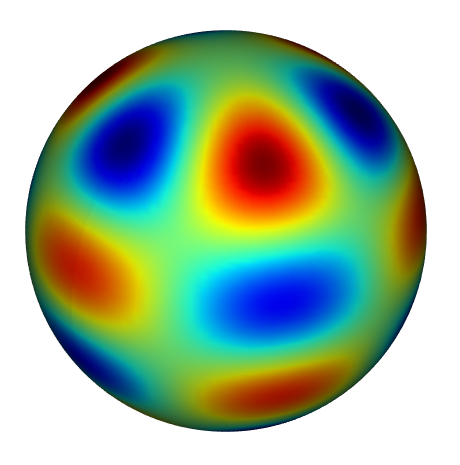
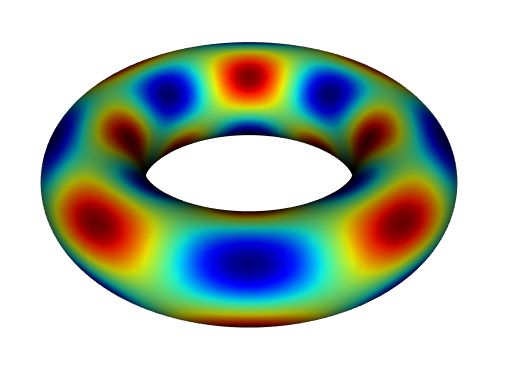
为了获得更迷幻的体验,请查看球体上Ginzburg-Landau方程的模拟(点击查看YouTube视频)

Shenfun还可以用来用全局谱基函数函数逼近解析函数,并在高度复杂的域上积分,例如下面的海螺壳,请参阅这个演示。

安装
Shenfun可以使用pip或conda安装,请参阅readthedocs上的安装章节。
依赖关系
在代码空间中尝试
尝试Shenfun的最简单方法是创建自己的代码空间。按此页上的绿色代码空间按钮,然后等待几分钟,让environment.yml中的所有内容安装完毕。然后在代码空间编辑器的终端中输入
source activate ./venv python setup.py build_ext -i echo -e "PYTHONPATH=/workspaces/shenfun" > .env
然后您就可以运行任何示例程序,或者例如尝试按照文档中的详细说明进行操作。我们假设您知道如何运行Python程序。请注意,如果您想在代码空间中使用例如IPython或Jupyter,则这些需要在venv环境中安装。
联系方式
对于评论、问题、错误报告和要求,请使用当前存储库的问题跟踪器,或查看readthedocs上的如何贡献?否则,主要作者可以通过以下方式联系
Mikael Mortensen mikaem at math.uio.no https://mikaem.github.io/ Department of Mathematics University of Oslo Norway
项目详情
shenfun-4.2.1.tar.gz的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | e5f9d2223e66689718d82676ee1fb73d0cbd59487bc148daf7807fff98d1c122 |
|
| MD5 | 65d0dedbf8069f093ff307f4459c7e00 |
|
| BLAKE2b-256 | 4e980e84083d38855a9303d6d9b00a62363511a4be74924ba58c3ab467bc81d8 |



