球面上的Mimetic INTerpolation
项目描述
MINT - 球面上的Mimetic INTerpolation
概述
此项目包含将源网格到目标网格重置边缘中心场代码。网格存储为网格单元集合,每个单元有四个顶点(即单元格是四边形)。边缘场作为沿每个边向量的积分存储。顶点坐标存储在经纬度空间。
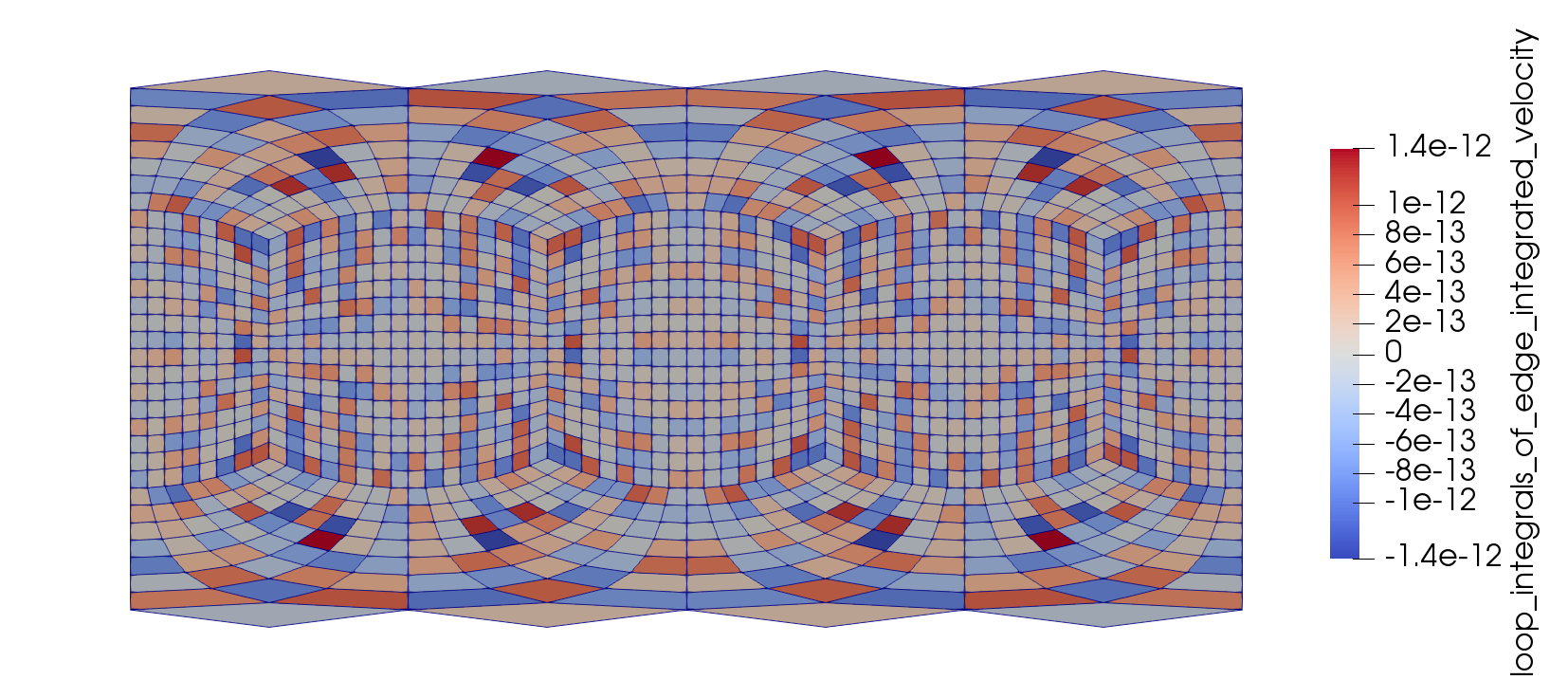
重置网格方法在Mimetic意义上满足Stokes定理,接近机器精度。特别是,由梯度得到的插值向场的环路积分为零。
先决条件
构建MINT Python模块
- 支持C++11的C++编译器
- Cython
- NetCDF库
- NumPy
- VTK
我们建议使用conda安装上述软件包。
构建MINT C++库和工具
- 支持C++11的C++编译器
- Fortran编译器(例如,gfortran 6.4)
- NetCDF库
- Doxygen
- VTK
如何构建MINT Python模块
《MINT》Python接口需要安装VTK、netCDF和tbb库。这最简单的方法是在conda环境中完成。
conda env create --file requirements/mint.yml
conda activate mint-dev
在根目录下的MINT目录中,然后输入:
pip install --no-deps --editable .
检查是否可以导入mint模块
python -c "import mint"
要运行测试,输入:
pytest
如何构建MINT C++库
执行以下操作以从Fortran、C或C++调用MINT
mkdir build
cd build
cmake ..
make -j 8
您可以使用以下方式指定编译器:
FC=mpif90 CXX=mpicxx cmake ..; make -j 8
通过输入以下内容,您可以检查构建是否成功:
make test
二进制工具
上述CMake构建将编译多个工具。要运行这些工具,请将MINT_SRC_DIR设置为您MINT源目录的位置(例如,export MINT_SRC_DIR=..)。
- 从经纬度网格计算到立方球体的插值权重
./tools/regrid_edges -s $MINT_SRC_DIR/data/latlon4x2.nc:latlon -S 0 \
-d $MINT_SRC_DIR/data/cs_4.nc:physics -D 1 \
-w weights.nc
- 通过加载先前生成的权重,将字段
edge_integrated_velocity从经纬度重新网格化到立方球体
./tools/regrid_edges -s $MINT_SRC_DIR/data/latlon4x2.nc:latlon -S 0 \
-d $MINT_SRC_DIR/data/cs_4.nc:physics -D 1 \
-v edge_integrated_velocity -W weights.nc -o edge_integrated_velocity.vtk
- 一步计算权重和重新网格化
./tools/regrid_edges -s $MINT_SRC_DIR/data/latlon4x2.nc:latlon -S 0 \
-d $MINT_SRC_DIR/data/cs_4.nc:physics -D 1 \
-v edge_integrated_velocity -W -o edge_integrated_velocity.vtk
- 重新网格化具有高度的时间相关字段
./tools/regrid_edges -s $MINT_SRC_DIR/data/lonlatzt_8x4x3x2.nc:mesh2d -S 0 \
-d $MINT_SRC_DIR/data/c24_u_integrated.nc:physics -D 1 \
-v u@$MINT_SRC_DIR/data/lonlatzt_8x4x3x2.nc \
-O regridedges_xyzt.nc -o regridedges_xyzt.vtk
API文档
如果您想从C、Python或Fortran调用MINT,这将非常有用
https://pletzer.github.io/mint/html/
守恒误差
下面的图表显示了通过为每个单元计算闭合线积分得到的拟微分重新网格化误差。
项目详情
关闭
python-mint-1.15.4.tar.gz的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 57ae186ee2ba1b328e310226ab91869394c56d1ec42616b70eea3f1f0d0a3a89 |
|
| MD5 | 2710f4144a7585e973879392f6378dd1 |
|
| BLAKE2b-256 | 4521385157524f0f970218470c0ad399ad38ce564eb024ae351797388b85084e |