原始MININEC天线优化代码的Python版本
项目描述
这是尝试用Python重写原始MININEC3基本源代码的尝试。标准用例如馈线阻抗和远场计算已实现并经过相当好的测试。仅提供命令行界面。
使用命令行界面的一个示例使用Cebik最初提出的12单元Yagi/Uda天线(没有电阻元件加载,并对元件长度进行轻微修正以使天线对称,Cebik文章中的显示错误可能是由于显示负数时精度不如正数的问题)。可以通过调用pymininec并使用--help选项来获取进一步的帮助。12单元天线的命令行选项(也可在文件test/12-el.pym中找到)为:
pymininec -f 148 \ -w 22,-.51943,0.00000,0,.51943,0.00000,0,.00238 \ -w 22,-.50165,0.22331,0,.50165,0.22331,0,.00238 \ -w 22,-.46991,0.34215,0,.46991,0.34215,0,.00238 \ -w 22,-.46136,0.64461,0,.46136,0.64461,0,.00238 \ -w 22,-.46224,1.03434,0,.46224,1.03434,0,.00238 \ -w 22,-.45989,1.55909,0,.45989,1.55909,0,.00238 \ -w 22,-.44704,2.19682,0,.44704,2.19682,0,.00238 \ -w 22,-.43561,2.94640,0,.43561,2.94640,0,.00238 \ -w 22,-.42672,3.72364,0,.42672,3.72364,0,.00238 \ -w 22,-.41783,4.53136,0,.41783,4.53136,0,.00238 \ -w 22,-.40894,5.33400,0,.40894,5.33400,0,.00238 \ -w 22,-.39624,6.0452,0,.39624,6.0452,0,.00238 \ --theta=0,5,37 --phi=0,5,73 \ --excitation-pulse=33 > 12-el.pout
当命令行选项在文件中时,可以添加注释(使用行首的‘#’)。Linux用户可以使用以下方式运行此操作(我相信Windows用户可以在Windows上找到类似的命令行)
pymininec $(sed '/^#/d' test/12-el.pym) > 12-el.pout
或使用grep
pymininec $(grep -v '#' test/12-el.pym) > 12-el.pout
此操作将从 .pym 文件中删除注释,并将结果作为命令行参数传递给 pymininec。结果输出文件包含电流、馈点阻抗和天线远场(以 dBi 为单位)的表格。输出试图重现 Mininec 原始基本实现的格式。
使用方法
存在一个 -h 或等效的 --help 选项,该选项提供了可用的选项的简要总结。所有长选项都可以缩写为其最短唯一前缀。值通常跟随选项,可以是选项和值之间的一个单独的参数(选项和值之间有一个空格),或者直接连接到选项上 =,请参见引言中的示例。
频率
典型用法使用 -f 或 --frequency 选项定义频率,频率以 MHz 为单位指定。此外,定义频率扫描通常也很有意义:扫描的起始频率是 -f 选项给出的值,使用选项 --frequency-increment=<increment> 和 --frequency-steps=<steps> 指定执行多少步长为 increment 的大小。
几何形状
接下来定义天线的几何形状。在当前版本中,只能指定导线。导线定义的格式为
--wire [tag,]<nseg>,<x1>,<y1>,<z1>,<x2>,<y2>,<z2>,<radius>
其中 (x1, y1, z1) 指定导线的第一个端点在笛卡尔坐标系中的位置,(x2, y2, z2) 定义导线的第二个端点,最后指定半径。所有长度和坐标均为米,但请参见下面的 --geo-scale 选项。前导标签是可选的,用于通过其他选项引用导线,例如指定馈点或天线上的负载。如果没有指定标签,导线从最高的指定标签编号开始编号,如果没有指定标签,则从一编号。建议不要混合带标签和无标签的导线。参数 nseg 指定将导线分割成多少段进行计算。
默认情况下,导线被分割成等长的段。段不应超过最短波长 λ 的 1/20。Mininec 通常会生成略高于谐振频率的结果(因此天线过长),这可以通过使用大量段来改进。
段长度渐变
另一种选择是使用不等长度的段。这可以通过使用 --taper-wire 选项来完成。它接受 2–4 个参数。第一个是标识应进行长度渐变的导线标签。第二个参数指定从导线的哪个端开始渐变。端可以是 1、2 分别代表第一和第二个端,3 代表两端。第三个和第四个参数分别指定最小和最大段长度。强制执行最小段长度为半径的 2.5 倍:如果段变短,则违反了细线假设,结果将会错误。渐变从在最小和最大段长度约束下可能的最短段开始,直到达到最大长度,它还停止使段变长,以保持段的数量。
几何变换
有时需要修改几何形状的一部分。有三种几何变换选项可供选择。要旋转天线的一部分或全部,可以使用--geo-rotate选项。它接收4-5个以逗号分隔的参数。第一个是一个用于排序几何变换的数字键:变换的顺序很重要,因此需要指定顺序。接下来的三个选项是围绕X轴、Y轴和Z轴的旋转。可选的第五个参数指定要旋转的地理对象标签(例如,线标签)。如果没有指定标签,则整个天线旋转。如果超过一个旋转不为零,则首先执行X轴旋转,然后是Y轴旋转,最后是Z轴旋转。
--geo-translate选项再次接收4-5个以逗号分隔的参数。第一个是一个排序键。接下来的三个参数指定X轴、Y轴和Z轴方向的位移。最后,还可以指定一个标签以定义要平移的几何对象。如果省略,则整个天线移动。这通常用于修改天线在地面上方的高度:整个天线可以向上移动,而无需编辑所有几何元素的Z组件。
最后,--geo-scale选项将所有几何参数(包括半径)按给定因子缩放。因子是第一个参数,可选的第二个参数再次提供几何标签。如果省略标签,则整个天线缩放。缩放始终是最后应用的,这样--geo-translate选项才适用于原始长度。
示例在test/vdipole-rot-trans.pym中:这具有几何变换选项
--geo-rotate=1,0,0,90 --geo-rotate=2,90,0,0 --geo-translate=3,0,0,7.33
首先将天线围绕Z轴旋转90°(排序键1),然后围绕X轴旋转90°(排序键2),最后整个天线向上移动7.33米(排序键3)。请注意,在这种情况下,我们不能将围绕Z轴和X轴的旋转组合成一个单独的--geo-rotate选项,因为这会首先围绕X轴旋转,这会导致与首先围绕Z轴旋转不同的结果。
脉冲
Mininec使用“脉冲”的概念来定义馈电电压和负载的应用位置。将脉冲视为两个段之间的点。这意味着在线的“末端”(除非有第二条或第三条线连接到那里)没有脉冲。因此,由3个段组成的单线只包含2个脉冲,或者一般来说,由N个段组成的线包含N-1个脉冲。脉冲自动编号,从1开始。
当定义一条新线,连接到已存在的线段的末端,该线段尚未连接,此时该线的接点脉冲由新线“拥有”:它成为新线上的第一个脉冲。
如果超过两条线在一个坐标处连接,将馈电点或负载分配给该脉冲不是一个好主意:馈电点或负载将仅在两条或三条以上线之间。在这种情况下,最好在放置馈电点或负载的位置插入一小段线,如图所示。
馈电点
对于天线至少需要定义一个馈电点。这使用--excitation-pulse选项来完成。脉冲编号是相对于天线所有脉冲的绝对值,或者可以指定一个由两个值组成的逗号分隔序列,其中第一个是相对于由第二个值指定的线标签的脉冲编号。默认情况下,激励电压为1V,但可以通过指定--excitation-voltage选项来更改,该选项接收以伏特为单位的复数。如果定义了多个馈电点,则通过多个--excitation-pulse和--excitation-voltage选项来完成。
集中负载
向天线结构添加负载是一个两步的过程。第一步定义负载。第二步将它们连接到脉冲上。
最简单的负载类型可以通过-l或--load选项指定。它需要一个复数作为参数。注意,这种简单的负载类型不会随频率而改变。在连接负载时,简单的负载会被首先排序。
拉普拉斯负载是最通用的负载类型。使用它,可以模拟集中参数负载的组合。在串联和并联集中组件的组合中,电感用L*s表示,电容用1/(C*s)表示,电阻用R表示。分析完一个复杂电路后,s的多项式结果会在分数的分子和分母中。分母使用--laplace-load-a选项指定,分子使用--laplace-load-b选项指定。两者都接受用逗号分隔的实数列表,表示按指数幂递增的多项式系数。在连接负载时,拉普拉斯负载会被最后排序。
另一个在内部基于拉普拉斯负载的负载类型可以通过--rlc-load选项指定。它需要三个参数,分别是欧姆中的电阻、亨利中的电感和法拉中的电容。法拉位置为零表示短路而不是电容。所有三个集中组件都是串联连接的。在连接负载时,RLC负载会被第二个排序。
最后是陷波负载——在内部也是基于拉普拉斯负载的——允许在天线中指定陷波。它由一个电阻与电感(模拟实际电感的非零电阻)的串联,与电容并联组成。--trap-load选项接受三个用逗号分隔的实数,分别是电阻、电感和法拉中的电容。陷波负载在连接负载时会被第三个排序。
使用--attach-load选项将负载连接到脉冲上。该选项接受2-3个用逗号分隔的参数。第一个是负载索引。负载索引是通过遍历所有简单负载,然后是所有RLC负载,然后是所有陷波负载,最后是所有拉普拉斯负载来计算的,从1开始分配负载索引。
线上的分布式负载
非理想导线具有分布式电导率。可以使用--skin-effect-conductivity选项指定导线的分布式电导率。或者,如果已知导线的电阻率,可以使用--skin-effect-resistivity选项。两个选项都接受一个或两个参数。第一个参数分别是电导率或电阻率。第二个可选参数指定几何形状(例如,导线)标记。如果没有给出标记,则皮肤效应负载连接到所有几何对象。
导线可以有绝缘层。使用--insulation-load选项模拟绝缘对导线分布式阻抗的影响。它接受2-3个参数。第一个参数指定包括绝缘层的导线半径。第二个指定绝缘的相对介电常数。第三个可选参数指定几何形状(例如,导线)标记。如果没有给出标记,则绝缘负载连接到所有导线。
每个导线最多可以指定一个绝缘负载和一个皮肤效应负载。
接地和辐射状导线
可以使用--medium选项指定地面。如果没有指定,则默认为空闲空间。可以指定多个--medium选项,在这种情况下,后续的媒体要么围绕第一个地面同心分布,要么在X方向上线性分配。--boundary选项指定媒体是否同心(--boundary=circular)或在X方向上(--boundary=linear)。默认为线性边界。--medium选项需要3-4个以逗号分隔的参数:介电常数(介电常数)、电导率和高度。如果前三个为零,则假设为理想地面。对于理想地面,仅允许一个--medium选项。
第四个参数给出了地面的宽度(到下一个媒体的距离),对于线性边界是X方向的长度,对于圆形边界是半径。最后一个--medium选项不使用第四个参数。
请注意,通常您希望更外层的媒体高度为负值,这可以模拟山峰。Mininec允许指定更高的地面,但结果将是有疑问的,因为没有对较高地面的反射进行建模。第一个媒体必须始终在高度零。
对于第一个媒体,可以指定径向。仅对非理想地面允许径向。选项--radial-count给出径向的数量。选项--radial-radius给出径向线的半径。指定径向将自动选择圆形边界。径向的长度由到下一个媒体的距离定义。因此,至少需要两个--medium选项。
指定计算的内容
使用--option选项可以指定要计算和打印的输出。此选项可以指定多次。它可以接受far-field、far-field-absolute、near-field和none等参数。当仅指定none作为唯一选项时,只打印电流和馈点阻抗。
far-field选项选择以dBi打印远场。far-field-absolute选项选择以V/m打印远场。此选项可以通过使用–ff-power`选项指定不同的功率水平,并通过使用--ff-distance选项指定远场测量点的径向距离来修改。远场测量是在使用--theta和--phi选项分别指定的仰角和方位角时进行的。仰角theta是从天顶测量的,而方位角phi是从X轴测量的。这两个选项都接受三个以逗号分隔的参数:起始角度、角度增量以及角度数量。默认情况下,theta是“0,10,10”,因此以10度步长从天顶运行到地面。phi的默认值是“0,10,37”,因此以10度步长绕方位圈运行,X轴上的0°和360°值计算两次。这是为了满足某些3d绘图工具绘制3d增益图案闭合表面的需要。
使用 --option=near-field 指定打印近场。这还需要指定 --near-field 选项,它包含9个以逗号分隔的参数:前三个定义近场测量的起始坐标(x,y,z),接下来的三个定义远场测量的增量,最后的三个定义每个方向上的增量数。使用 --nf-power 选项可以修改近场计算的电平。
如果没有任何 --option,则如果没有近场选项,将打印远场。
其他选项
使用 --output-cmdline 选项可以打印给定的命令行选项。这在测试和使用API时很有用:所有选项都可以写出来以重现当前的设置。此选项需要一个文件名作为参数。
使用 --output-basic-input 选项,可以打印原始Mininec代码在Basic中的输入。Basic代码使用提示来请求用户输入。使用此选项可以生成完整的用户输入。通过运行Yabasi并使用 -i 选项将用户输入馈入Basic程序,这对于比较pymininec计算出的值和原始Basic代码计算出的值很有用。此选项需要一个文件名作为参数。
使用 -T 或 --timing 选项,请求打印计算中各个部分的运行时间。此选项不需要参数。
测量计时
从版本1开始,有一个命令行选项 -T,它在标准错误输出上输出计算计时。这被用于测量最近计算矢量化结果。速度提升大约是
阻抗矩阵计算的约50倍。因此,12元素Yagi/Uda的22个段每个元素的计算时间从大约23秒降低到0.44秒。
远场计算的约200倍。因此,12元素Yagi/Uda的方位角和仰角分辨率为5°的计算时间从大约19秒降低到0.09秒。即使是1°分辨率的计算,对于这个天线也只需要不到2秒。
近场计算的约5倍。这可以通过分块批处理近场坐标来进一步改进。我目前不太使用近场计算,因此进一步的改进将等待我有更多需求...
绘图
pymininec生成的输出表对于了解天线的远场行为不太有用。曾经与pymininec捆绑在一起的使用plot-antenna的程序现在已转移到其自己的项目中。您现在可以绘制天线的仰角和方位角图、3D图、几何形状和VSWR。所有这些都可以作为独立程序(使用matplotlib)或作为HTML导出到浏览器(使用plotly)。
测试覆盖率和代码质量
本节包含有关代码质量以及最近改进的一些说明。
测试覆盖率:确保与原始Mininec一致
针对原始Basic源代码进行了几项测试,测试用例请参阅子目录test。其中一项测试用例是一个简单的7MHz线天线偶极子,波长一半,分为10段。在一种情况下,导线厚度为0.01m(1cm),我们使用这样粗的导线是为了使mininec代码更努力工作,因为它不能使用细导线假设。另一个测试是针对细导线的情况。还添加了来自原始Mininec报告的倒L型和T型天线。所有这些都可以作为示例。目前测试语句覆盖率已达100%。
如果Python版本低于3.10,则pytest框架会标记某行代码未被覆盖。这是在compute_impedance_matrix函数末尾的一个continue语句(截至本文写作的第1388行)。这是Python版本低于3.10时的一个bug:在Python调试器上设置continue语句的断点时,尽管continue语句被正确执行,但断点永远不会到达。一种解决方案是在continue语句之前放置一个虚拟赋值,并验证测试覆盖率现在报告continue语句已被覆盖。我已经在pytest项目中报告了这个bug,并在python中报告了这个bug,由于Python3.9不再维护,这两个bug现在已被关闭。
对于所有测试示例,都仔细验证了结果与Basic原始结果相近(参见在Basic中运行示例以了解如何在21世纪运行原始Basic代码)。差异是由于Basic中单精度实现与Python中双精度实现相比的舍入误差造成的。在可能的情况下,我使用了numpy中的数值代码来加速计算,例如,通过使用numpy.linalg.solve而不是逐行从Basic翻译来求解阻抗矩阵。您可以自己验证差异。在test目录中,有扩展名为.mini的输入文件,这些文件(在转换为回车换行约定后)旨在作为原始Basic代码的输入。Basic代码的输出在扩展名为.bout的文件中,而Python代码的输出在扩展名为.pout的文件中。回归测试中比较了.pout文件。在test目录中的.pym文件是用于使用mininec.py重新创建.pout文件的命令行参数。如果区分大小写,使用Yabasi生成的输出使用大写扩展名.Bout。
在Zeineddin的论文[5]中,他研究了比较近场和远场时的数值不稳定性。他通过在双精度算术中进行某些近场计算来解决此问题。我试图复制这些实验,并在Basic版本中可以重现数值不稳定性。在Python版本中,不存在这种不稳定性(因为一切都是双精度)。但Python计算出的绝对场值低于Zeineddin(以及Basic代码)报告的值。
Python代码中的电流计算似乎没有问题,计算出的电流值低于Basic,导致场值较低。但比较两个版本的阻抗矩阵时,误差非常低,请参见test_matrix_fill_ohio_example测试,位于test/test_mininec.py中,以及plot_z_errors过程用于绘制test/ohio.py中的误差(以百分比表示)。与NEC计算出的值相比,Basic代码对近场和远场产生略高的值,而Python代码产生的值略低于NEC。我尚未在NEC中尝试模拟这一点。
您可以在test/ohio*中找到文件(论文是在俄亥俄大学完成的)。这次有一个python脚本ohio.py,用于计算近场和远场值,无需重新计算阻抗矩阵。此脚本可以在一个图中显示近场和远场值,并在第二个图中显示差异。计算了两个距离,因此代码生成了四个图。还有一个脚本用于绘制Basic近场和远场差异plot_bas_ohio.py。
向量化前的代码质量
向量化之前,代码的状态是这样的
当前的Python代码仍然难以理解 - 它是Basic逐行翻译的结果,尤其是在我还未能理解代码意图的地方。对于变量名,它们可能(尚未)反映代码的意图。我已经将诸如计算复数的角度、计算绝对值或复数的乘除等操作移至python中相应的复数算术,我在检测到模式时进行了这些操作。
因此,代码的“去意大利面化”在某些部分尚未成功 :-) 我的逆向工程笔记可以在文件basic-notes.txt中找到,其中解释了mininec中使用的某些变量和一些子例程,以及(主要从REM语句中获取的)Basic代码的描述。
代码仍然相当慢:Cebik在建模示例中使用的12元素Yagi/Uda天线是一个例子,在我的PC上(该PC具有264个段,比原始Mininec支持的段数多)需要大约50秒(我使用theta和phi角度的5度增量时),对于1度角度大约需要11分钟(!)原因是一切目前都像Basic一样实现为嵌套循环。这应该(并且可以)改为使用numpy中的矢量和矩阵运算。在矩阵填充操作的内部循环中,使用高斯求积或椭圆积分的数值解计算了几个积分。这些现在使用来自scipy.integrate和scipy.special.ellipk的方法(或至少在高斯求积的情况下是常数)实现。
向量化后的代码质量
在开始向量化之前,我将隐式脉冲计算(这使用了一个非常复杂的索引方案来访问脉冲信息)更改为显式数据结构在mininec/pulse.py中。这大大提高了代码的可理解性(使我能够进一步重构以向量化计算)。
当前版本仍然保留着来自Basic实现的模糊变量名,而且在很多情况下,计算过程中的中间值含义并不明确。由于Basic没有复数,计算的语义只能猜测。我希望在获得[2]版本时改进这个问题——版本ADA181682包含许多难以阅读的页面。如果您有更好的可读性版本的报告,请告诉我!
多反转-V示例
1998年Carol F. Milazzo博士(KP4MD)的一个旧网页中有用Mininec模拟的天线示例。这些示例中的第一个是三个交叉的反转-V(其中一个具有负载电感以增加有效长度)。pymininec的模拟结果与KP4MD使用的基于Mininec的NEC4WIN相当。但看起来NEC4WIN可能将打印的“Diam.”作为线的半径(参见网站上的图1),作为半径(参见附录中的天线模型文件)。至少,如果这个格式是从NEC继承下来的,那么线定义的最后列将包含半径,这种格式的解释也与Pymininec的模拟结果更加一致。以下表格显示了原始数据与在Pymininec中使用原始模型直径的一半(“Pymininec r”)和直径作为半径(Pymininec 2r)的比较。当使用(假设)直径作为半径时,输出数据与网站数据更匹配。
频率 |
原始 |
Pymininec r |
Pymininec 2r |
|
7MHz |
增益方位角 |
-2.42 dBi |
-2.52 dBi |
-2.49 dBi |
增益仰角 |
7.21 dBi |
7.21 dBi |
7.21 dBi |
|
阻抗 |
38.74 +6.77j |
38.82 -3.66j |
39.28 +1.49j |
|
14MHz |
增益方位角 |
4.33 dBi |
4.60 dBi |
4.37 dBi |
增益仰角 |
7.23 dBi |
7.73 dBi |
7.38 dBi |
|
阻抗 |
46.16 -326j |
31.86 -307j |
43.00 -313j |
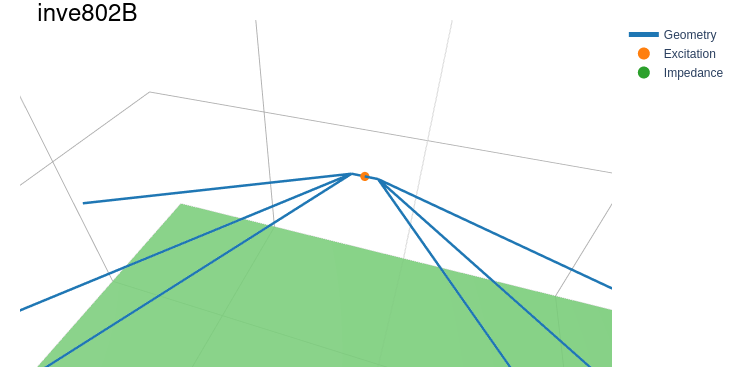
KP4MD的所有示例都已转换为Pymininec,并作为inve802B.pym、hloop40-14.pym、hloop40-7.pym、vloop20.pym和lzh20.pym在test目录中提供。只有使用反转-V的inve802B.pym(原始示例中的直径作为Pymininec中的半径)使用原始示例中的直径作为半径,其他所有示例都使用原始示例中的值的一半(应该是直径)作为半径。但大多数示例在半径加倍时与KP4MD计算出的值更匹配。
剑的另一面
有一些新测试检查馈点阻抗与文献中的已知计算。特别是与这个节标题相同的Roy Lewallen的一篇旧文章[8]。
“Python”列来自pymininec,而“Basic Yabasi”列是使用我的Basic解释器Yabasi运行的原始Basic实现。而“Basic pcbasic”列使用pcbasic解释器。
请注意,“弯偶极子”是水平弯曲的(不是倒V形),所有线端都处于同一高度。到目前为止,我还没有能够重现使用仅14段且结果与文章中所示相同(参见弯偶极子的条目 14*)的特殊分段方案。在试图完全重现它时,虚部要低得多(更多容量)。分段方案也不是很好:在mininec中,相邻段应该只有长度的2倍,而不是更多。特殊分段方案有一个5倍的跳跃,这可能导致数值不稳定,从而使我们得到双精度浮点数的结果差异很大。
对于弯偶极子,我进行了三个额外的实验:一个是从两端逐渐变细(条目 14t2),两个是从一端逐渐变细(条目 14t1 和 14t1l)。示例 14t1 对段长度没有限制,而条目 14t1l 强制段长度至少为1/200波长的最小值。在所有一端逐渐变细的情况下,馈点端的最小段长度。这些实验中没有哪一个接近论文中的14段实验。
直偶极子
段 |
Lewallen |
Python |
基本 Yabasi |
基本 pcbasic |
10 |
74.073+20.292j |
74.074+20.298j |
74.074+20.298j |
74.074+20.300j |
20 |
75.870+21.877j |
75.872+21.897j |
75.872+21.897j |
75.872+21.897j |
30 |
76.573+23.218j |
76.567+23.169j |
76.567+23.169j |
76.572+23.203j |
40 |
76.972+24.053j |
76.972+24.052j |
76.972+24.052j |
76.973+24.068j |
50 |
77.222+24.517j |
77.240+24.647j |
77.240+24.647j |
弯偶极子
段 |
Lewallen |
Python |
基本 Yabasi |
基本 pcbasic |
10 |
11.509-76.933j |
11.498-77.045j |
11.498-77.045j |
11.498-77.044j |
20 |
11.751-53.812j |
11.740-53.929j |
11.740-53.929j |
11.740-53.932j |
30 |
11.819-46.934j |
11.808-47.068j |
11.808-47.068j |
11.808-47.055j |
40 |
11.848-43.783j |
11.837-43.893j |
11.837-43.893j |
11.838-43.858j |
50 |
11.861-41.988j |
11.851-42.107j |
11.851-42.107j |
|
14* |
11.312-43.119j |
11.104-47.879j |
||
14t1 |
10.859-42.486j |
|||
14t1l |
11.118-46.593j |
|||
14t2 |
11.314-45.659j |
|||
运行测试
你可以使用以下方法运行测试:
python3 -m pytest test
如果需要报告覆盖率,则变为:
python3 -m pytest --cov mininec test
要获取更详细的覆盖率报告,请使用:
python3 -m pytest --cov-report term-missing --cov mininec test
这将显示未由测试覆盖的行的详细报告。
皮肤效应负载
[本节使用 ReStructuredText 中的数学,可能无法在所有平台上正确渲染。特别是,GitHub 关于此有一个已开放十多年的问题[83]。据说它在 pypi 中得到支持[12062],让我们看看。]
为了支持几何对象(例如导线)上的皮肤效应负载,我们需要计算段的内部阻抗。Wikipedia 上关于皮肤效应的文章给出了每单位长度的内部阻抗的以下公式:
其中
并且 \(r\) 是半径,\(J_v\) 是第一类贝塞尔函数的阶数 \(v\)。 \(Z_\Int\) 是导线的每单位长度阻抗。
由于Wikipedia上关于皮肤效应的文章引用了这本书,但我无法获取,所以我查阅了经典著作 Chipman 的传输线理论和问题[9],其中给出了 \(Z_\Int\) 的以下公式(第77页6.27)。
其中
并且 \(\delta\) 为皮肤深度(见公式6.15,第74页)
以及 \(\alpha\) 为半径。注意,此公式与NEC-2 Fortran实现中使用的公式相同,如我在博客文章中推导的(见[10]),但与NEC理论文章中描述的公式不同(第75页),这在我的博客文章[10]中有详细说明。
Chipman [9] 还有一个从Kelvin函数到Bessel函数的转换(见第74页的公式6.11和6.12)
其中 \(\Re\) 是复数的实部,\(\Im\) 是复数的虚部。在一个表达式中,这可以写成
对于导数,我们有
因此,对于Kelvin函数的分数
将此代入上面的 \( Z_\Int \) 公式中,我们得到
利用事实
我们得到
将 \( R_s \) 和 \( \delta \) 代入并使用 \( \rho=1/\sigma \)
用 \( k \) 替换上面并使用
当我们将 \( a=r \) 代入时,这等同于维基百科中的公式。这是pymininec中用于处理皮肤效应负载的公式。
关于在此处使用Kelvin函数而不是Bessel函数的历史的说明:在袖珍计算器时代之前,已经有Kelvin函数的现成表格。由于无法通过表格查找复杂函数的参数,因此更倾向于使用带有数学表格的书籍进行计算...
绝缘导线
绝缘导线使用分布电感等效半径
其中 \( a \) 是导线的原始半径,\( b \) 是包括绝缘层的导线半径,\( \varepsilon_r \) 是绝缘材料的相对介电常数,\( \mu_0 \) 是真空磁导率,\( a_e \) 是等效半径。电感 \( L \) 是绝缘导线(或导线段)的单位长度的电感。
这个公式最初出现在吴的论文中[12]。我是通过Steve Stearns,K6OIK的笔记发现它的,这个笔记实际上是ARRL天线手册[13]的补充。
我最初尝试了Roy Lewallen,W7EL(EZNEC的作者)建议的Richmond的公式[15]。但这个公式对于小段来说数值上不稳定。更多细节在我的博客[16]中。
椭圆积分参数笔记
Mininec代码在计算阻抗矩阵以及在几个其他地方使用椭圆积分的实现。积分使用一组E向量的系数,在不同的地方引用不同。在开源Basic代码的最新版本中,这些参数位于第1510-1512行。它们也印在关于该版本Mininec的出版物[2]中,其中列出了Basic源代码(与在线版本略有不同),在p. C-31的第1512-1514行。
1.38629436112 |
.09666344259 |
.03590092383 |
.03742563713 |
.01451196212 |
.5 |
.12498593397 |
.06880248576 |
.0332835346 |
.00441787012 |
在关于Mininec的第一篇出版物[1]中,作者在第13页给出了参数
1.38629436112 |
.09666344259 |
.03590092383 |
.03742563713 |
.01451196212 |
.5 |
.1249859397 |
.06880248576 |
.03328355346 |
.00441787012 |
这与Mininec代码第3版的后续论文[2]在第9页给出的参数一致,但该论文的大部分内容是从早期论文中复制粘贴过来的。
第一篇论文[1]列出了该版本的Basic代码,在第48页参数给出如下
1.38629436 |
.09666344 |
.03590092 |
.03742563713 |
.01451196 |
.5 |
.12498594 |
.06880249 |
.0332836 |
.0041787 |
在每种情况下,第一行是a参数,第二行是b参数。《em》参数在所有版本中都是一致的,但请注意,在b参数(第二行)中,当前Basic代码在第二列多了一个3。早期Basic代码的四舍五入表明,第二个3是后来Basic版本中的一个错误。此外,请注意,在第四列,后来Basic代码比论文中的版本少了5。早期Basic代码的四舍五入也表明,后来的Basic代码有误。
椭圆积分参数的错误对Mininec代码计算的值影响不大。有一些细微的差异,但这些差异低于Basic和Python实现之间的差异(单精度与双精度算术)。我曾希望这与众所周知的事实有关,即Mininec找到的天线谐振点比实际高一些百分比,这意味着通常在实际应用中,计算的线长略长。显然并非如此。当线径小于波长的1e-4时,非常细的线下的谐振点也是错误的,这发生在线径小于波长的1e-4时。即使在那种情况下——在该椭圆积分没有使用的情况下——谐振也是稍微错误的。
两份报告中引用的椭圆积分参数的参考文献[3]在第591页列出了以下表格
1.38629436112 |
.09666344259 |
.03590092383 |
.03742563713 |
.01451196212 |
.5 |
.12498593597 |
.06880248576 |
.03328355346 |
.00441787012 |
请注意,我只能找到1972年的手册版本,而不是报告中提到的1980年版本。因此,这些参数可能在后续版本中得到修正的可能性很小。结果是,报告在第四列是正确的,而基本程序是错误的。但第二列仍然包含另一个版本,请注意,逗号后的第9位是5,而不是基本程序中的3,也不是Mininec报告中缺少的数字[1] [2]。
由于我无法确定手册中是否有错别字[3],我进一步挖掘:手册引用了Hastings的《数字计算机的近似方法》(未给出年份)[4]。我找到的那本书版本是1955年的,系数列在172页。
1.38629436112 |
.09666344259 |
.03590092383 |
.03742563713 |
.01451196212 |
.5 |
.12498593597 |
.06880248576 |
.03328355346 |
.00441787012 |
因此,显然手册[3]是正确的。而基本版本和两个Mininec报告至少有一个错别字。
自从这段文字写成以来,椭圆积分的实现已被删除,并替换为对scipy.special.ellipk的调用。计算输出的差异比基本(单精度)和Python(双精度)实现之间的差异要小。
在Basic中运行示例
原始Basic源代码今天仍然可以运行。
感谢Rob Hagemans的pcbasic项目,我有了调试初始pymininec实现的起点。它是用Python编写的,可以使用pip安装。它也被包含在一些Linux发行版中,例如在Debian中。
在此期间,我周末写了自己的Basic解释器,名为Yabasi,原因有两个
pcbasic忠实地再现了当时的内存限制
pcbasic在单精度浮点数计算上做了些努力
第三个原因在我使Yabasi工作起来时显现:它比pcbasic快得多。
由于Mininec从命令行读取天线仿真的所有输入,我在Basic中创建包含可重复的命令行输入的天线仿真输入文件。这样的脚本示例在dipole-01.mini中,后缀mini表示Mininec文件。这些可以直接用Yabasi运行(使用-i选项),要使用pcbasic运行,需要将其转换为回车换行符结束。Makefile中有代码做这个,例如,你可以运行
make vertical-rad.CR
并创建test/vertical-rad.mini的回车版本。
当然,只有实际用mininec basic代码运行这些输入文件才有意义,因为这将显示所有提示。请注意,我不得不修改Basic代码中某些数组的尺寸,以避免在pcbasic Basic解释器中遇到内存不足的情况。
您可以使用命令行选项 --input= 运行 pcbasic,以指定输入文件。请注意,输入文件必须转换为回车换行符结束(没有换行符)。我在 对pcbasic的贡献 中描述了如何使用Python调试器调试Basic代码,这部分内容已移至 pcbasic wiki。
对于 Yabasi,这种调试是内置的,您可以通过指定命令行选项 -L <line> 来指定要停止的Basic代码中的行号,其中 <line> 是您希望停止的行号。停止后,您可以
!self.break_lineno = 'all'
逐行执行Basic程序。或者,您也可以指定另一个要停止的行号。
在文件 debug-basic.txt 中,您可以找到我使用Python调试器和pcbasic调试mininec的笔记。这基本上是一个随机的剪切和粘贴缓冲区。
原始的Basic源代码曾经可以在PA3KJ的 非官方NEC档案 或同一作者 Mininec github项目 中找到,该非官方NEC档案网站似乎在此写作时遇到了问题(空页面)。
我在github上有一个修补过的 MININEC 版本,该版本从 Mininec github项目 分支,并做了一些小的修复,
使用更大的 DIM 语句
修复了椭圆积分参数,并使用更好的精度来处理椭圆曲线和高斯求积参数
使用更好的精度来处理硬编码的常量 1/log(10)*10,这在远场计算期间使用(以获取dBi)。这使得 MININEC 的远场结果更好地匹配Python实现。
发布说明
v1.1: 功能改进
为实施进一步几何对象(不仅仅是线)奠定基础
线(和未来的几何对象)可以有标签,现在所有线、段、脉冲和负载的使用现在都使用一个标签,这是一个从1开始的自动计算数字,可以显式指定为线;标签用于所有错误消息
添加段长度渐变:现在可以将线分成不等长的段
添加皮肤效应负载
添加绝缘线负载
添加几何变换旋转、平移和缩放
实现命令行参数的往返,允许输出当前设置作为命令行选项
实现输出Basic输入以测试天线模型与原始Basic实现的对比
将 --excitation-segment 选项重命名为 --excitation-pulse,现在它允许指定相对于几何对象(例如线)的脉冲
v1.0: 通过向量化提高速度
向量化远场计算
向量化阻抗矩阵的计算
向量化近场计算
v0.6.1: 修复脚本入口点
v0.6.0: 添加pyproject.toml
添加pyproject.toml
添加LICENSE文件
小修
v0.5.0: 修复错误和新的负载类型
新增负载类型 RLC 负载和陷波负载:前者使用串联 R-L-C(每个均可选),后者使用串联回路的 R-L 并联 C(以更好地模拟天线中的陷波)
线端匹配中的错误修复:如果有多条线连接到单个点,则之前的实现不会正确构建数据结构
添加更多回归测试
弃用 unittest 以避免 unittest 和 pytest 测试框架的混合
v0.4.0:将 plot-antenna 拆分为独立项目
独立项目 plot-antenna
修复解析多个中等选项,在文档中提及地面
v0.3.0:正确实现了拉普拉斯负载
使用 scipy.special.ellipk 进行椭圆积分
使用 scipy.integrate 中的高斯求积系数
测试共振(NEC 与 mininec)
v0.2.0:添加关于新绘图程序的简短段落
测试覆盖率
表达式简化
v0.1.0:初始发布
文献
项目详情
下载文件
下载适合您平台的文件。如果您不确定选择哪个,请了解更多关于 安装包 的信息。
源分布
构建分布
pymininec-1.1.0.tar.gz 的散列
| 算法 | 散列摘要 | |
|---|---|---|
| SHA256 | 06de0805682680c743c9be5909dea40abb43770b6e538643d36e3f1fb56628b1 |
|
| MD5 | ad97eb8a075ec871a506e215c8a0fb1b |
|
| BLAKE2b-256 | b5a492c0b68d8d9ae06d424859b0c394e731ae2cddebba5f7e3a23a8bdefa71c |
pymininec-1.1.0-py3-none-any.whl 的散列
| 算法 | 散列摘要 | |
|---|---|---|
| SHA256 | 5b43c24a2ab1f3dc5a18c8aa2a4a8f58ec874e83c484e86aa6bfff2793925fe0 |
|
| MD5 | 0647e440abf182c337d1527f4042e579 |
|
| BLAKE2b-256 | 96d8a7d40ffb8f4ef5fcde2cbe9e6655b691a0eaac4657924ec9130d9a3a0622 |



