OEIS

项目

此项目是实现OEIS中的一些序列。

用法

要安装它，请运行：pip install oeis。

命令行使用

oeis可以从命令行使用

$ oeis --help
usage: oeis [-h] [--list] [--start START] [--stop STOP] [--plot] [--random] [--file] [--dark-plot] [sequence]

Print a sweet sequence

positional arguments:
  sequence       Define the sequence to run (e.g.: A181391)

optional arguments:
  -h, --help     show this help message and exit
  --list         List implemented series
  --start START  Define the starting point of the sequence.
  --stop STOP    End point of the sequence (excluded).
  --plot         Print a sweet sweet sweet graph
  --random       Pick a random sequence
  --file         Generates a png of the sequence's plot
  --dark-plot    Print a dark dark dark graph

需要特定的序列吗？

$ oeis A000108
# A000108

Catalan numbers: C(n) = binomial(2n,n)/(n+1) = (2n)!/(n!(n+1)!).
    Also called Segner numbers.

[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190]

懒惰？随机选择一个

$ oeis --random
# A000045

Fibonacci numbers: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1.

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

想看些酷的东西吗？

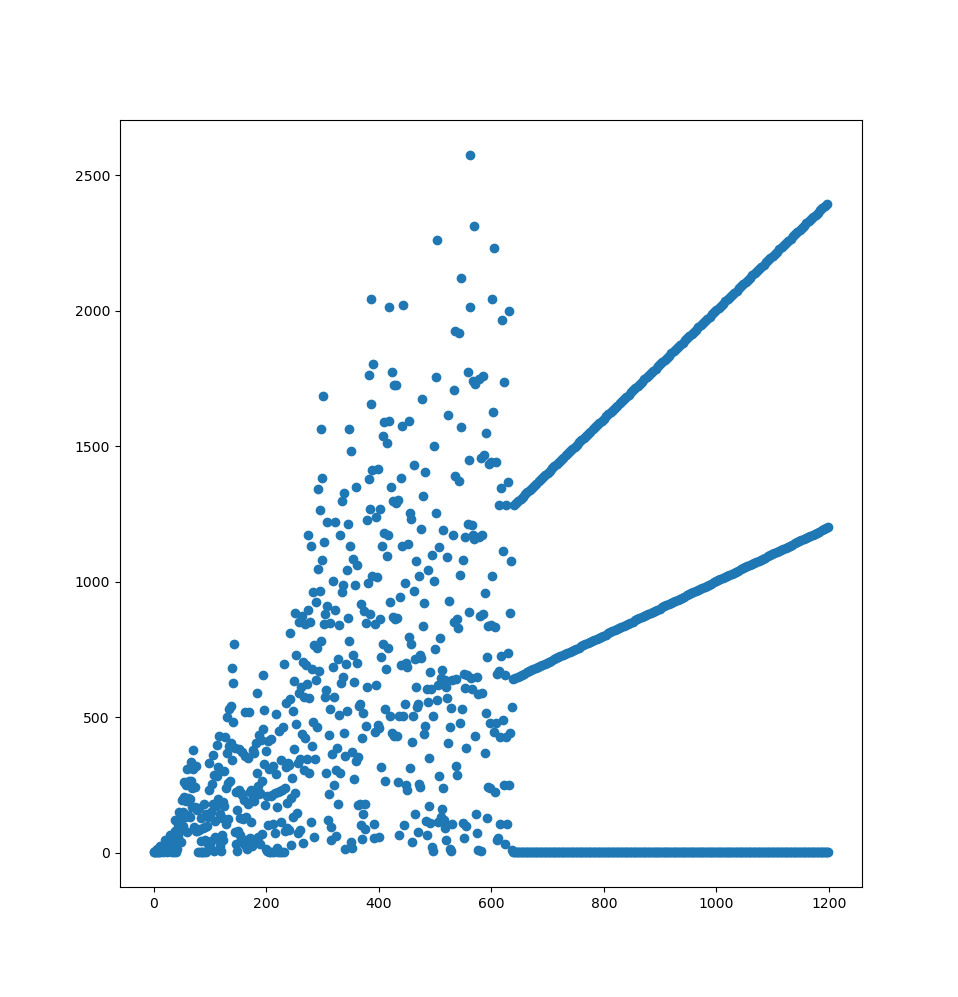
$ oeis A133058 --plot --stop 1200

库使用

oeis模块将序列公开为Python序列

>>> from oeis import A000045
>>> print(*A000045[:10], sep=", ")
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55
>>> A000045[1] == A000045[2]
True
>>> A000045[100:101]
[354224848179261915075]

贡献

我们使用black编码风格，并使用tox运行一些测试，因此创建一个venv并在其中安装tox后，运行tox -p auto它应该看起来像这样

$ tox -p auto
✔ OK mypy in 11.807 seconds
✔ OK flake8 in 12.024 seconds
✔ OK black in 12.302 seconds
✔ OK py37 in 15.344 seconds
✔ OK py38 in 21.041 seconds
✔ OK py39 in 21.042 seconds
______________________________________ summary ________________________________________
  py37: commands succeeded
  py38: commands succeeded
  py39: commands succeeded
  flake8: commands succeeded
  mypy: commands succeeded
  black: commands succeeded
  congratulations :)

实现一个系列的两种方式：将其实现为函数，或将其实现为生成器。

从函数实现系列

对于结果只依赖于其位置的序列，如A004767，它是a(n) = 4*n + 3，作为函数来说非常直接，使用@oeis.from_function()作为装饰器来设置管道

@oeis.from_function()
def A004767(n: int) -> int:
    """Integers of a(n) = 4*n + 3."""
    return 4 * n + 3

它具有快速直接访问的优势

print(A004767[1_000_000])

可以通过调用您的函数一次来完成。

注意：没有“偏移校正”是神奇地完成的。如果偏移是 1，不要期望你的函数在 n=0 时被调用。

从生成器实现序列

有些序列需要前一个（或前几个）值来计算，它们不能轻易地作为函数实现，你可以将它们作为生成器实现，在这种情况下使用 @oeis.from_generator() 装饰器

@oeis.from_generator()
def A000045() -> Iterable[int]:
    """Fibonacci numbers: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1."""
    a, b = (0, 1)
    yield 0
    while True:
        a, b = b, a + b
        yield a

注意：只需返回实际的序列值，不要在意偏移量，例如，尝试通过返回 None 或 0 来移动结果。

比较

所以，为了清楚起见，这两种实现是严格等价的

@oeis.from_generator()
def A008589() -> Iterable[int]:
    """Multiples of 7."""
    return (n * 7 for n in count())

@oeis.from_function()
def A008589(n: int) -> int:
     """Multiples of 7."""
     return n * 7

如果偏移量是1，只有生成器会从1开始（函数不需要改变，因为1会作为参数给出）

@oeis.from_generator(offset=1)
def A008589() -> Iterable[int]:
    """Multiples of 7."""
    return (n * 7 for n in count(1))

为什么要求没有固定？

项目通常固定的有两种要求

• 实际项目依赖（numpy，...）。
• 测试依赖（pytest，...）。

无论如何，用户只是 pip install（或 apt install 或其他）项目并期望它工作。如果与依赖项存在不兼容性，我们需要知道它并在 install_requires 中明确限制。

固定项目依赖项是一种谎言：它在CI中有效，但在用户环境中可能无效。

固定测试依赖项看起来很舒适，就像测试今天通过明天也会通过一样，但这也意味着大多数时间都在运行过时的linters。

最后，固定依赖项可能根本不可能：可能不存在一组冻结的依赖项可以在你想要测试的每个Python版本上工作。

所以想法是：让我们不固定任何东西，在用户发现问题之前先从困难中学到问题。

是的，这意味着CI可能会随时崩溃。但比最终用户发现错误要好。