nvector库是一个用Python编写的工具套件,用于解决地理位置计算,源自nvector。
项目描述
nvector库是一个用Python编写的工具套件,用于解决地理位置计算。目前实现了以下操作:
计算两个地理位置之间的表面距离。
将一个参考系中给出的位置转换为另一个参考系。
给定起点、方位角/航向和距离,找到目标点。
找到多个地理位置的平均位置(中心/中点)。
找到两条路径的交点。
找到路径与位置之间的交叉距离。
使用n-vector,计算变得简单且非奇异。对于任何全球位置(以及任何距离),都实现了全精度。
描述
在这个库中,我们使用“n矢量”来表示位置,这是地球模型(与纬度和经度相同的参考椭球体)的法线矢量。当使用n矢量时,所有地球位置都被同等对待,无需担心奇点或间断。使用n矢量的一个额外好处是,许多位置计算可以通过简单的矢量代数(例如点积和叉积)来解决。
使用提供的函数,在n矢量与纬度/经度之间转换是明确且简单的。
n_E是程序代码中的n矢量,而在文档中我们使用nE。E表示一个地球固定位置坐标系,它表示n矢量的三个分量沿着E的三个轴。
有关符号和参考系的其他详细信息,请参阅文档。
官方文档
http://www.navlab.net/nvector/
http://nvector.readthedocs.io/en/latest/
- Kenneth Gade (2010)
尖端技术:https://github.com/pbrod/nvector。
官方版本可在以下网址获取:http://pypi.python.org/pypi/nvector。
安装nvector
如果您已安装pip并且处于在线状态,则只需输入
$ pip install nvector
以获取最新稳定版本。使用pip的优势在于所有要求都自动安装。
您可以通过以下方式将nvector及其所有依赖项下载到“pkg”文件夹中
$ pip install –download=pkg nvector
要安装已下载的nvector,只需输入
$ pip install –no-index –find-links=pkg nvector
验证安装
要验证nvector是否可通过Python访问,请在您的shell中输入python。然后在Python提示符下,尝试导入nvector
>>> import nvector as nv >>> print(nv.__version__) 0.7.7dev0
要测试工具箱是否正常工作,请将以下内容粘贴到交互式Python会话中
import nvector as nv
nv.test('--doctest-modules')
或
$ py.test –pyargs nvector –doctest-modules
在命令提示符下。
入门指南
以下是一些常见大地测量问题的面向对象解决方案。在第一个示例中,还给出了功能解决方案。其他问题的功能解决方案可以在教程的功能示例部分找到。
示例1:“从A到B的delta”
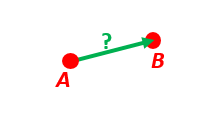
给定两个位置,A和B,它们相对于地球E的纬度、经度和深度。
找出两个位置之间的确切矢量(以米为单位,向北、向东和向下),并找出相对于北方的方向(方位角)。假设WGS-84椭球体。给定的深度是从椭球面起算的。使用位置A来定义北方、东方和下方的方向。(由于地球的曲率和指向北极的不同方向,北方、东方和下方的方向(相对于地球)会改变。为了定义北方和东方方向,位置A必须位于两极之外。)
- 解决方案
>>> import numpy as np >>> import nvector as nv >>> wgs84 = nv.FrameE(name='WGS84') >>> pointA = wgs84.GeoPoint(latitude=1, longitude=2, z=3, degrees=True) >>> pointB = wgs84.GeoPoint(latitude=4, longitude=5, z=6, degrees=True)
- 步骤1:找到p_AB_N(在N中分解的delta)。
>>> p_AB_N = pointA.delta_to(pointB) >>> x, y, z = p_AB_N.pvector.ravel() >>> 'Ex1: delta north, east, down = {0:8.2f}, {1:8.2f}, {2:8.2f}'.format(x, y, z) 'Ex1: delta north, east, down = 331730.23, 332997.87, 17404.27'- 步骤2:同时找到相对于北方的方向(方位角)到B
>>> 'azimuth = {0:4.2f} deg'.format(p_AB_N.azimuth_deg) 'azimuth = 45.11 deg' >>> 'elevation = {0:4.2f} deg'.format(p_AB_N.elevation_deg) 'elevation = 2.12 deg' >>> 'distance = {0:4.2f} m'.format(p_AB_N.length) 'distance = 470356.72 m'- 功能解决方案
>>> import numpy as np >>> import nvector as nv >>> from nvector import rad, deg
>>> lat_EA, lon_EA, z_EA = rad(1), rad(2), 3 >>> lat_EB, lon_EB, z_EB = rad(4), rad(5), 6
- 步骤1:转换为n矢量
>>> n_EA_E = nv.lat_lon2n_E(lat_EA, lon_EA) >>> n_EB_E = nv.lat_lon2n_E(lat_EB, lon_EB)
- 步骤2:找到p_AB_E(在E中分解的delta)。WGS-84椭球体是默认值
>>> p_AB_E = nv.n_EA_E_and_n_EB_E2p_AB_E(n_EA_E, n_EB_E, z_EA, z_EB)
- 步骤3:找到位置A的R_EN
>>> R_EN = nv.n_E2R_EN(n_EA_E)
- 步骤4:找到p_AB_N(在N中分解的delta)。
>>> p_AB_N = np.dot(R_EN.T, p_AB_E).ravel() >>> x, y, z = p_AB_N >>> 'Ex1: delta north, east, down = {0:8.2f}, {1:8.2f}, {2:8.2f}'.format(x, y, z) 'Ex1: delta north, east, down = 331730.23, 332997.87, 17404.27'- 步骤5:同时找到相对于北方的方向(方位角)到B
>>> azimuth = np.arctan2(y, x) >>> 'azimuth = {0:4.2f} deg'.format(deg(azimuth)) 'azimuth = 45.11 deg'>>> distance = np.linalg.norm(p_AB_N) >>> elevation = np.arcsin(z / distance) >>> 'elevation = {0:4.2f} deg'.format(deg(elevation)) 'elevation = 2.12 deg'>>> 'distance = {0:4.2f} m'.format(distance) 'distance = 470356.72 m'- 另请参阅
示例2:“从B和delta到C”
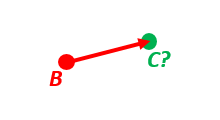
连接到车辆B(本体坐标系)的雷达或声纳测量到物体C的距离和方向。我们假设距离和两个角度(通常是相对于B的方位角和仰角)已经组合到矢量p_BC_B(即从B到C的矢量,在B中分解)。B的位置由n_EB_E和z_EB给出,B的定向(姿态)由R_NB给出(此旋转矩阵可以通过使用zyx2R从偏航/俯仰/滚转得到)。
以n向量形式和深度(n_EC_E和z_EC)找到对象C的精确位置,假设地球椭球体半长轴为a和扁率f。对于WGS-72,使用a = 6 378 135 m和f = 1/298.26。
- 解决方案
>>> import numpy as np >>> import nvector as nv >>> wgs72 = nv.FrameE(name='WGS72') >>> wgs72 = nv.FrameE(a=6378135, f=1.0/298.26)
- 步骤1:B的位置和方向在E上方400米处给出
>>> n_EB_E = wgs72.Nvector(nv.unit([[1], [2], [3]]), z=-400) >>> frame_B = nv.FrameB(n_EB_E, yaw=10, pitch=20, roll=30, degrees=True)
- 步骤2:在B中将ΔBC分解
>>> p_BC_B = frame_B.Pvector(np.r_[3000, 2000, 100].reshape((-1, 1)))
- 步骤3:在E中将ΔBC分解
>>> p_BC_E = p_BC_B.to_ecef_vector()
- 步骤4:通过将ΔBC加到EB上找到点C
>>> p_EB_E = n_EB_E.to_ecef_vector() >>> p_EC_E = p_EB_E + p_BC_E >>> pointC = p_EC_E.to_geo_point()
>>> lat, lon, z = pointC.latlon_deg >>> msg = 'Ex2: PosC: lat, lon = {:4.4f}, {:4.4f} deg, height = {:4.2f} m' >>> msg.format(lat, lon, -z) 'Ex2: PosC: lat, lon = 53.3264, 63.4681 deg, height = 406.01 m'- 另请参阅
示例3:“ECEF向量到大地纬度”
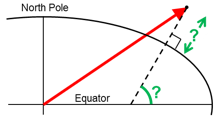
位置B以“ECEF向量”p_EB_E给出(即从E,地球中心到B的向量,在E中分解)。假设WGS-84椭球体,找到大地纬度、经度和高度(latEB、lonEB和hEB)。
- 解决方案
>>> import numpy as np >>> import nvector as nv >>> wgs84 = nv.FrameE(name='WGS84') >>> position_B = 6371e3 * np.vstack((0.9, -1, 1.1)) # m >>> p_EB_E = wgs84.ECEFvector(position_B) >>> pointB = p_EB_E.to_geo_point()
>>> lat, lon, z = pointB.latlon_deg >>> 'Ex3: Pos B: lat, lon = {:4.4f}, {:4.4f} deg, height = {:9.3f} m'.format(lat, lon, -z) 'Ex3: Pos B: lat, lon = 39.3787, -48.0128 deg, height = 4702059.834 m'- 另请参阅
示例4:“大地纬度到ECEF向量”
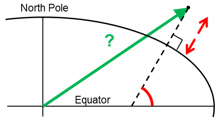
给定位置B的大地纬度、经度和高度作为latEB、lonEB和hEB,找到此位置对应的ECEF向量p_EB_E。
- 解决方案
>>> import nvector as nv >>> wgs84 = nv.FrameE(name='WGS84') >>> pointB = wgs84.GeoPoint(latitude=1, longitude=2, z=-3, degrees=True) >>> p_EB_E = pointB.to_ecef_vector()
>>> 'Ex4: p_EB_E = {} m'.format(p_EB_E.pvector.ravel().tolist()) 'Ex4: p_EB_E = [6373290.277218279, 222560.20067473652, 110568.82718178593] m'- 另请参阅
示例5:“地表距离”
找到两个位置A和B之间的地表距离sAB(即大圆距离)。忽略A和B的高度,即如果它们不为零高度,我们寻求位于地球表面的点之间的距离,直接位于A和B上方/下方。还应找到欧几里得距离(弦长)dAB。使用地球半径6371e3 m。将结果与WGS-84椭球体的精确计算进行比较。
- 球体的解决方案
>>> import numpy as np >>> import nvector as nv >>> frame_E = nv.FrameE(a=6371e3, f=0) >>> positionA = frame_E.GeoPoint(latitude=88, longitude=0, degrees=True) >>> positionB = frame_E.GeoPoint(latitude=89, longitude=-170, degrees=True)
>>> s_AB, azia, azib = positionA.distance_and_azimuth(positionB) >>> p_AB_E = positionB.to_ecef_vector() - positionA.to_ecef_vector() >>> d_AB = p_AB_E.length
>>> msg = 'Ex5: Great circle and Euclidean distance = {}' >>> msg = msg.format('{:5.2f} km, {:5.2f} km') >>> msg.format(s_AB / 1000, d_AB / 1000) 'Ex5: Great circle and Euclidean distance = 332.46 km, 332.42 km'- 替代球体解决方案
>>> path = nv.GeoPath(positionA, positionB) >>> s_AB2 = path.track_distance(method='greatcircle') >>> d_AB2 = path.track_distance(method='euclidean') >>> msg.format(s_AB2 / 1000, d_AB2 / 1000) 'Ex5: Great circle and Euclidean distance = 332.46 km, 332.42 km'
- WGS84椭球体的精确解决方案
>>> wgs84 = nv.FrameE(name='WGS84') >>> point1 = wgs84.GeoPoint(latitude=88, longitude=0, degrees=True) >>> point2 = wgs84.GeoPoint(latitude=89, longitude=-170, degrees=True) >>> s_12, azi1, azi2 = point1.distance_and_azimuth(point2)
>>> p_12_E = point2.to_ecef_vector() - point1.to_ecef_vector() >>> d_12 = p_12_E.length >>> msg = 'Ellipsoidal and Euclidean distance = {:5.2f} km, {:5.2f} km' >>> msg.format(s_12 / 1000, d_12 / 1000) 'Ellipsoidal and Euclidean distance = 333.95 km, 333.91 km'- 另请参阅
示例6:“插值位置”
给定B在时间t0和t1的位置,n_EB_E(t0)和n_EB_E(t1)。
找到时间ti的插值位置n_EB_E(ti)。所有位置都以n向量给出。
- 解决方案
>>> import nvector as nv >>> wgs84 = nv.FrameE(name='WGS84') >>> n_EB_E_t0 = wgs84.GeoPoint(89, 0, degrees=True).to_nvector() >>> n_EB_E_t1 = wgs84.GeoPoint(89, 180, degrees=True).to_nvector() >>> path = nv.GeoPath(n_EB_E_t0, n_EB_E_t1)
>>> t0 = 10. >>> t1 = 20. >>> ti = 16. # time of interpolation >>> ti_n = (ti - t0) / (t1 - t0) # normalized time of interpolation
>>> g_EB_E_ti = path.interpolate(ti_n).to_geo_point()
>>> lat_ti, lon_ti, z_ti = g_EB_E_ti.latlon_deg >>> msg = 'Ex6, Interpolated position: lat, lon = {:2.1f} deg, {:2.1f} deg' >>> msg.format(lat_ti, lon_ti) 'Ex6, Interpolated position: lat, lon = 89.8 deg, 180.0 deg'- 向量化解决方案
>>> t = np.array([10, 20]) >>> nvectors = wgs84.GeoPoint([89, 89], [0, 180], degrees=True).to_nvector() >>> nvectors_i = nvectors.interpolate(ti, t, kind='linear') >>> lati, loni, zi = nvectors_i.to_geo_point().latlon_deg >>> msg.format(lat_ti, lon_ti) 'Ex6, Interpolated position: lat, lon = 89.8 deg, 180.0 deg'
- 另请参阅
示例7:“平均位置”
三个位置A、B和C分别以n向量n_EA_E、n_EB_E和n_EC_E给出。找到平均位置M,以n_EM_E给出。请注意,该计算与位置深度无关。
- 解决方案
>>> import nvector as nv >>> points = nv.GeoPoint(latitude=[90, 60, 50], ... longitude=[0, 10, -20], degrees=True) >>> nvectors = points.to_nvector() >>> n_EM_E = nvectors.mean() >>> g_EM_E = n_EM_E.to_geo_point() >>> lat, lon = g_EM_E.latitude_deg, g_EM_E.longitude_deg >>> msg = 'Ex7: Pos M: lat, lon = {:4.4f}, {:4.4f} deg' >>> msg.format(lat, lon) 'Ex7: Pos M: lat, lon = 67.2362, -6.9175 deg'- 另请参阅
示例8:“A和B的方位/距离”
我们有初始位置A,相对于北方的航向(顺时针)和最终沿大圆行进距离sAB。使用地球半径6371e3 m找到目的地B。
在地球测量学中,这被称为“第一个地球测量问题”或“球体的直接地球测量问题”,我们看到这与示例2相似,但现在Δ是作为航向和大圆距离给出的。 (“球体的第二个/逆地球测量问题”已在示例1和5中解决。)
- 精确解决方案
>>> import numpy as np >>> import nvector as nv >>> frame = nv.FrameE(a=6371e3, f=0) >>> pointA = frame.GeoPoint(latitude=80, longitude=-90, degrees=True) >>> pointB, azimuthb = pointA.displace(distance=1000, azimuth=200, degrees=True) >>> lat, lon = pointB.latitude_deg, pointB.longitude_deg
>>> msg = 'Ex8, Destination: lat, lon = {:4.4f} deg, {:4.4f} deg' >>> msg.format(lat, lon) 'Ex8, Destination: lat, lon = 79.9915 deg, -90.0177 deg'>>> np.allclose(azimuthb, -160.01742926820506) True
- 大圆解决方案
>>> pointB2, azimuthb = pointA.displace(distance=1000, ... azimuth=200, ... degrees=True, ... method='greatcircle') >>> lat2, lon2 = pointB2.latitude_deg, pointB.longitude_deg >>> msg.format(lat2, lon2) 'Ex8, Destination: lat, lon = 79.9915 deg, -90.0177 deg'
>>> np.allclose(azimuthb, -160.0174292682187) True
- 另请参阅
示例9:“两条路径的交点”
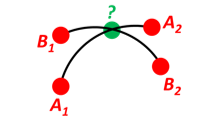
定义从两个给定位置(在球形地球的表面上)的路径,即通过这两点的最短距离圆。
路径A由A1和A2给出,而路径B由B1和B2给出。
找到两个大圆交点的位置C。
- 解决方案
>>> import nvector as nv >>> pointA1 = nv.GeoPoint(10, 20, degrees=True) >>> pointA2 = nv.GeoPoint(30, 40, degrees=True) >>> pointB1 = nv.GeoPoint(50, 60, degrees=True) >>> pointB2 = nv.GeoPoint(70, 80, degrees=True) >>> pathA = nv.GeoPath(pointA1, pointA2) >>> pathB = nv.GeoPath(pointB1, pointB2)
>>> pointC = pathA.intersect(pathB) >>> pointC = pointC.to_geo_point() >>> lat, lon = pointC.latitude_deg, pointC.longitude_deg >>> msg = 'Ex9, Intersection: lat, lon = {:4.4f}, {:4.4f} deg' >>> msg.format(lat, lon) 'Ex9, Intersection: lat, lon = 40.3186, 55.9019 deg'- 检查点C不在A1和A2之间或B1和B2之间
>>> pathA.on_path(pointC) False >>> pathB.on_path(pointC) False
- 检查点C在大圆路径A和路径B上
>>> pathA.on_great_circle(pointC) True >>> pathB.on_great_circle(pointC) True
- 另请参阅
示例10:“交叉距离”
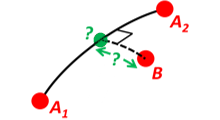
路径A由两个位置A1和A2给出(类似于前面的示例)。
找到路径A(即通过A1和A2的大圆)和位置B(即大圆与B之间的最短地表距离)之间的交叉距离sxt。
还找到B与由大圆定义的平面的欧几里得距离dxt。使用地球半径6371e3。
最后,找到大圆上的交点并确定它是否位于位置A1和A2之间。
- 解决方案
>>> import numpy as np >>> import nvector as nv >>> frame = nv.FrameE(a=6371e3, f=0) >>> pointA1 = frame.GeoPoint(0, 0, degrees=True) >>> pointA2 = frame.GeoPoint(10, 0, degrees=True) >>> pointB = frame.GeoPoint(1, 0.1, degrees=True) >>> pathA = nv.GeoPath(pointA1, pointA2)
>>> s_xt = pathA.cross_track_distance(pointB, method='greatcircle') >>> d_xt = pathA.cross_track_distance(pointB, method='euclidean')
>>> val_txt = '{:4.2f} km, {:4.2f} km'.format(s_xt/1000, d_xt/1000) >>> 'Ex10: Cross track distance: s_xt, d_xt = {}'.format(val_txt) 'Ex10: Cross track distance: s_xt, d_xt = 11.12 km, 11.12 km'>>> pointC = pathA.closest_point_on_great_circle(pointB) >>> np.allclose(pathA.on_path(pointC), True) True
- 另请参阅
致谢
为 Python 编写的 Python 的 FFI (挪威国防研究机构) 的 nvector 软件包是由 Per A. Brodtkorb 编写的,基于 FFI 的 nvector 工具箱,该工具箱是为 Matlab 编写的,由 FFI 的导航组编写。nvector.core 和 nvector.rotation 模块是对 matlab nvector 工具箱的矢量化重新实现,而 nvector.objects 模块是为 nvector 核心功能提供的新易于使用的面向对象用户界面,详细内容请参见 [GB20]。
大部分内容基于 K. Gade 的文章 [Gad10]。
因此,在出版物中使用此页面或下载的程序代码时,应引用本文。
然而,如果您使用了 FrameE.direct、FrameE.inverse、GeoPoint.distance_and_azimuth 或 GeoPoint.displace 中的任何一种方法,您还应引用 Karney 的文章 [Kar13],因为这些方法调用 Karney 的 geographiclib 库进行计算。
参考文献
K. Gade, 非奇异水平位置表示,航海,63(3):395-417,2010。
C.F.F. Karney. 大地测量的算法。大地测量学,87(1):43-55,2013。
K. Gade 和 P.A. Brodtkorb, Python 的 nvector 文档,2020。
项目详情
下载文件
下载适合您平台的文件。如果您不确定选择哪个,请了解有关 安装包 的更多信息。
源分布
构建分布
nvector-1.0.1.tar.gz 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | a693c46b45284bd6c1b75eb825117e0cfdef37ce977d7395c0a0248d5993a644 |
|
| MD5 | ad1ce9ba67416f8ca73c8a5aae27b7c1 |
|
| BLAKE2b-256 | 455e4a5fb9471805171eea375d3d5e4acd179eb008ce0ea5601fd64c7da2887d |










