Lambert问题求解器集合。
项目描述
lamberthub:Lambert问题求解器中心
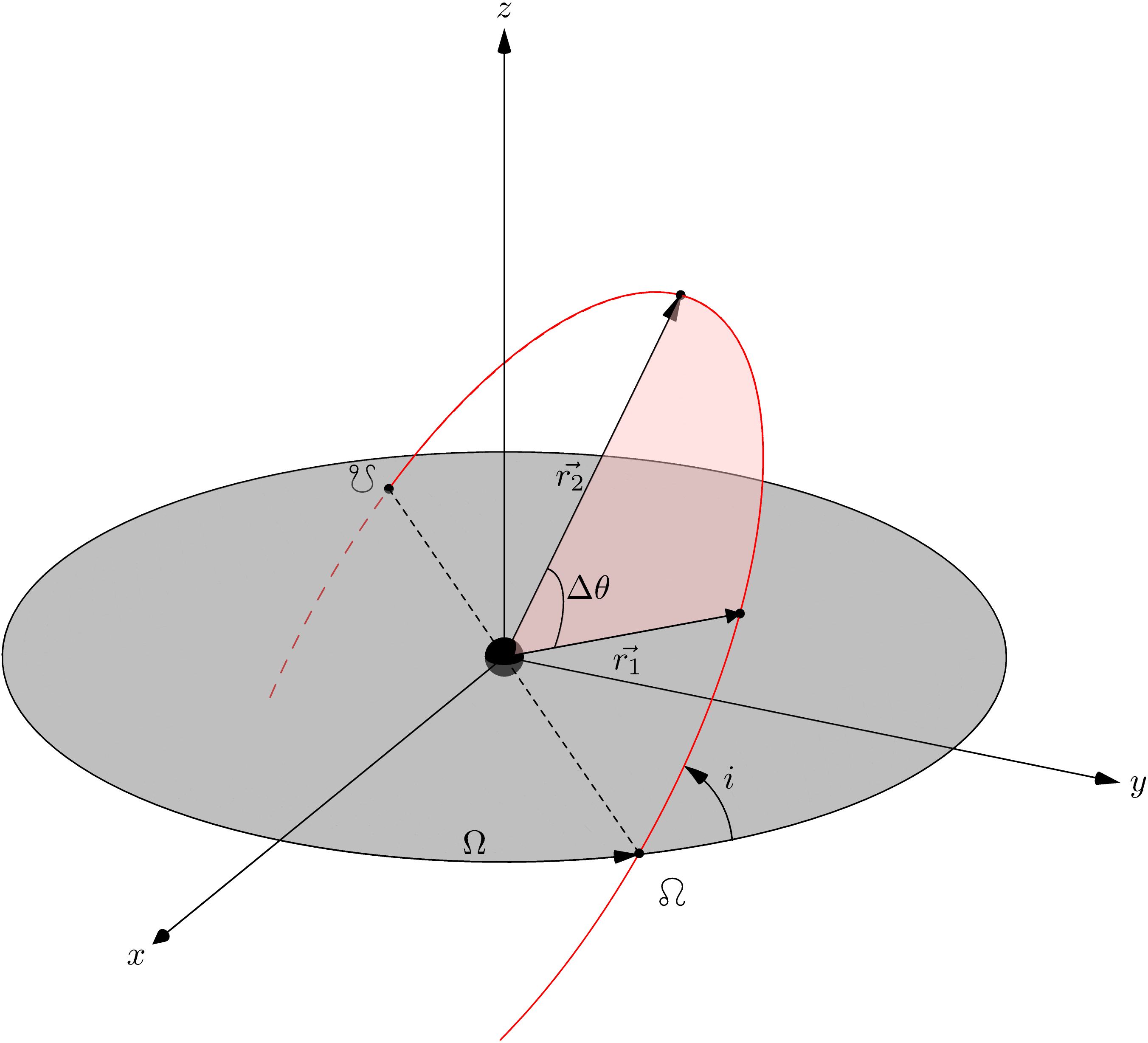
这是一个Python库,旨在提供解决Lambert问题(天体力学中的经典问题,涉及确定航天器在两个空间点之间飞行的时间及其轨道)的解决方案。该问题是轨道规划中至关重要的一环,尤其是对于星际任务。
此库实现了多个算法,每个算法以其作者和出版年份命名,用于解决Lambert问题的不同变体。这些算法可以处理不同类型的轨道,包括多圈路径和直接转移。
安装
支持多种安装方法
| 标志 | 平台 | 命令 |
|---|---|---|
 |
PyPI | python -m pip install lamberthub |
 |
GitHub | python -m pip install https://github.com/jorgepiloto/lamberthub/archive/main.zip |
可用的求解器
| 算法 | 参考 |
|---|---|
gauss1809 |
C. F. Gauss, 《天体力学理论,轨道为椭圆的球体表面》. 1809. |
battin1984 |
R. H. Battin 和 R. M. Vaughan, “一种优雅的 Lambert 算法,” 《制导、控制和动力学杂志》第 7 卷,第 6 期,第 662–670 页,1984。 |
gooding1990 |
R. Gooding, “求解 Lambert 轨道边值问题的一种方法,” 《天体力学与动力天文学》第 48 卷,第 2 期,第 145–165 页,1990。 |
avanzini2008 |
G. Avanzini, “一种简单的 Lambert 算法,” 《制导、控制和动力学杂志》第 31 卷,第 6 期,第 1587–1594 页,2008。 |
arora2013 |
N. Arora 和 R. P. Russell, “使用余弦变换的快速且稳健的多次旋转 Lambert 算法,” 《AAS 会议论文集》第 13 卷,第 728 页,2013。 |
vallado2013 |
D. A. Vallado, 《天体动力学基础与应用》. Springer 科学 & 商业媒体,2013,第 12 卷。 |
izzo2015 |
D. Izzo, “重新审视 Lambert 问题,” 《天体力学与动力天文学》第 121 卷,第 1 期,第 1–15 页,2015。 |
使用求解器
在 lamberthub 中实现的任何 Lambert 问题算法都是一个 Python 函数,该函数接受以下参数
from lamberthub import authorYYYY
v1, v2 = authorYYYY(
mu, r1, r2, tof, M=0, prograde=True, low_path=True, # Type of solution
maxiter=35, atol=1e-5, rtol=1e-7, full_output=False # Iteration config
)
其中 author 是开发了求解器的作者的姓名,YYYY 是出版年份。任何由 ALL_SOLVERS 列表托管的求解器。
参数
| 参数 | 类型 | 描述 |
|---|---|---|
mu |
float |
引力参数,即吸引物体的质量乘以万有引力常数。 |
r1 |
np.array |
初始位置向量。 |
r2 |
np.array |
最终位置向量。 |
tof |
float |
初始和最终向量之间的飞行时间。 |
M |
int |
旋转次数。如果为零(默认值),则假设直接转移。 |
prograde |
bool |
控制最终轨道的倾角。如果为 True,倾角在 0 到 90 度之间。如果为 False,倾角在 90 到 180 度之间。 |
low_path |
bool |
在有多种解决方案时选择路径类型。除非有任务约束,否则没有具体优势。 |
maxiter |
int |
计算解决方案时允许的最大迭代次数。 |
atol |
float |
迭代方法的绝对容差。 |
rtol |
float |
迭代方法的相对容差。 |
full_output |
bool |
如果为 True,则返回附加信息,例如迭代次数。 |
返回
| 返回 | 类型 | 描述 |
|---|---|---|
v1 |
np.array |
初始速度向量。 |
v2 |
np.array |
最终速度向量。 |
numiter |
int |
迭代次数(仅当 full_output 为 True 时)。 |
tpi |
float |
每次迭代的耗时(仅当 full_output 为 True 时)。 |
示例
示例:求解直接和顺行转移轨道
问题描述
假设你想求解星际飞行器的轨道(即太阳是主要吸引体),已知初始和最终位置分别为
\vec{r_1} = \begin{bmatrix} 0.159321004 \\ 0.579266185 \\ 0.052359607 \end{bmatrix} \text{ [AU]} \quad \quad
\vec{r_2} = \begin{bmatrix} 0.057594337 \\ 0.605750797 \\ 0.068345246 \end{bmatrix} \text{ [AU]} \quad \quad
飞行时间为 $\Delta t = 0.010794065$ 年。轨道为顺行和直接,因此 $M=0$。记住,当 $M=0$ 时,只有一个可能的解决方案,所以 low_path 标志在这个问题中不起任何作用。
解决方案
对于这个问题,使用 gooding1990。任何其他求解器也可以工作。接下来,实例化问题的参数。最后,计算初始和最终速度向量。
from lamberthub import gooding1990
import numpy as np
mu_sun = 39.47692641
r1 = np.array([0.159321004, 0.579266185, 0.052359607])
r2 = np.array([0.057594337, 0.605750797, 0.068345246])
tof = 0.010794065
v1, v2 = gooding1990(mu_sun, r1, r2, tof, M=0, prograde=True)
print(f"Initial velocity: {v1} [AU / years]")
print(f"Final velocity: {v2} [AU / years]")
结果
Initial velocity: [-9.303608 3.01862016 1.53636008] [AU / years]
Final velocity: [-9.511186 1.88884006 1.42137810] [AU / years]
直接取自《天体力学与轨道力学导论,修订版》由 R.H. Battin 编著的问题 7-12。
项目详情
下载文件
下载适合您平台的文件。如果您不确定选择哪个,请了解更多关于安装包的信息。
源代码发行版
lamberthub-1.0.0.tar.gz (47.7 kB 查看哈希值)
构建发行版
lamberthub-1.0.0-py3-none-any.whl (56.4 kB 查看哈希值)
关闭
lamberthub-1.0.0.tar.gz 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | cde13891f118dc51895d1a0c13cb9ae3c060d526429a789594427585bf431c91 |
|
| MD5 | 1629809de7758a70b7f8f26a34563adf |
|
| BLAKE2b-256 | 115392f74e57f1d375e04e4dd67a245079c09fc3bb0b81c992bedfc34a31e6b9 |
关闭
lamberthub-1.0.0-py3-none-any.whl 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 3a1f7ebadad9e325a8e06ae3da4680b716aeeb51c765debd9491267356c92ef4 |
|
| MD5 | 3095c2b668e68d729fd213d831c96786 |
|
| BLAKE2b-256 | 9cc151bdff9d1f2dbfbf9e772f20ac415f8d2040fd0c7c991bbb46c37ef2f05d |









