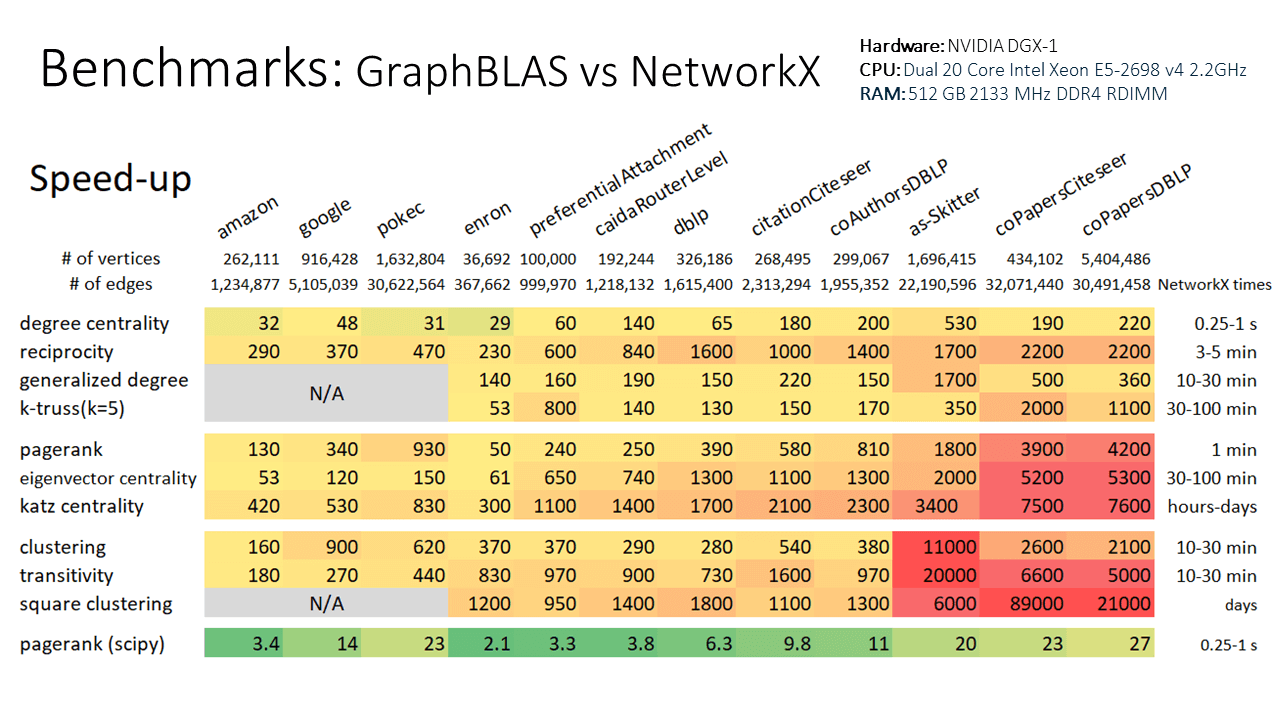
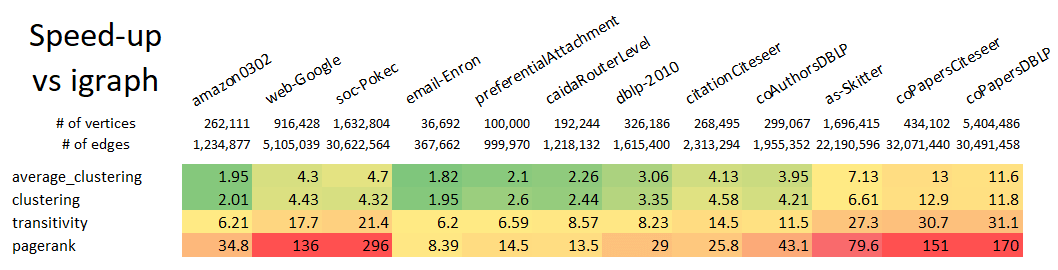
使用GraphBLAS编写的图算法和NetworkX的后端
项目描述
graphblas-algorithms 是一组使用 python-graphblas 编写的 GraphBLAS 算法。它可以直接使用或作为 NetworkX 的实验性 后端。
为什么使用 GraphBLAS 算法?因为它通过使用 NetworkX API,具有 快速、灵活 和 熟悉 的特性。
安装
conda install -c conda-forge graphblas-algorithms
pip install graphblas-algorithms
基本用法
首先,创建一个 GraphBLAS 矩阵。
import graphblas as gb
M = gb.Matrix.from_coo(
[0, 0, 1, 2, 2, 3],
[1, 3, 0, 0, 1, 2],
[1., 2., 3., 4., 5., 6.],
nrows=4, ncols=4, dtype='float32'
)
接下来将矩阵封装为 ga.Graph。
import graphblas_algorithms as ga
G = ga.Graph(M)
最后调用算法。
hubs, authorities = ga.hits(G)
当结果是每个节点的一个值时,将返回一个 gb.Vector。在 HITS 的情况下,返回两个向量,分别表示枢纽和权威值。
结果为子图算法的算法将返回 ga.Graph。
NetworkX 插件
将调用分配到插件是 Networkx 3.0 中的一个新功能。当在环境中安装了 networkx 和 graphblas-algorithms 时,可以调用 NetworkX 算法,并将它们分配到 graphblas-algorithms 中的等效版本。
分配示例
import networkx as nx
import graphblas_algorithms as ga
# Generate a random graph (5000 nodes, 1_000_000 edges)
G = nx.erdos_renyi_graph(5000, 0.08)
# Explicitly convert to ga.Graph
G2 = ga.Graph.from_networkx(G)
# Pass G2 to NetworkX's k_truss
T5 = nx.k_truss(G2, 5)
G2 不是一个 nx.Graph,但它有一个属性 __networkx_plugin__ = "graphblas"。这告诉 NetworkX 将 k_truss 调用分配给 graphblas-algorithms。这种链接的存在是因为 graphblas-algorithms 将自己注册为 "networkx.plugin" 入口点。
结果 T5 是一个表示原始图 5-truss 结构的 ga.Graph。要将它转换为 NetworkX 图,请使用
T5.to_networkx()
请注意,即使在 ga.Graph 之间进行转换,此示例的速度也比使用本地 NetworkX k-truss 实现快 10 倍。速度改进与图大小成比例,因此较大的图将相对于 NetworkX 获得更大的速度提升。
插件算法
以下 NetworkX 算法已由 graphblas-algorithms 实现,并可以使用上述分配模式使用。
graphblas_algorithms.nxapi
├── boundary
│ ├── edge_boundary
│ └── node_boundary
├── centrality
│ ├── degree_alg
│ │ ├── degree_centrality
│ │ ├── in_degree_centrality
│ │ └── out_degree_centrality
│ ├── eigenvector
│ │ └── eigenvector_centrality
│ └── katz
│ └── katz_centrality
├── cluster
│ ├── average_clustering
│ ├── clustering
│ ├── generalized_degree
│ ├── square_clustering
│ ├── transitivity
│ └── triangles
├── community
│ └── quality
│ ├── inter_community_edges
│ └── intra_community_edges
├── components
│ ├── connected
│ │ ├── is_connected
│ │ └── node_connected_component
│ └── weakly_connected
│ └── is_weakly_connected
├── core
│ └── k_truss
├── cuts
│ ├── boundary_expansion
│ ├── conductance
│ ├── cut_size
│ ├── edge_expansion
│ ├── mixing_expansion
│ ├── node_expansion
│ ├── normalized_cut_size
│ └── volume
├── dag
│ ├── ancestors
│ └── descendants
├── dominating
│ └── is_dominating_set
├── efficiency_measures
│ └── efficiency
├── generators
│ └── ego
│ └── ego_graph
├── isolate
│ ├── is_isolate
│ ├── isolates
│ └── number_of_isolates
├── isomorphism
│ └── isomorph
│ ├── fast_could_be_isomorphic
│ └── faster_could_be_isomorphic
├── linalg
│ ├── bethehessianmatrix
│ │ └── bethe_hessian_matrix
│ ├── graphmatrix
│ │ └── adjacency_matrix
│ ├── laplacianmatrix
│ │ ├── laplacian_matrix
│ │ └── normalized_laplacian_matrix
│ └── modularitymatrix
│ ├── directed_modularity_matrix
│ └── modularity_matrix
├── link_analysis
│ ├── hits_alg
│ │ └── hits
│ └── pagerank_alg
│ ├── google_matrix
│ └── pagerank
├── lowest_common_ancestors
│ └── lowest_common_ancestor
├── operators
│ ├── binary
│ │ ├── compose
│ │ ├── difference
│ │ ├── disjoint_union
│ │ ├── full_join
│ │ ├── intersection
│ │ ├── symmetric_difference
│ │ └── union
│ └── unary
│ ├── complement
│ └── reverse
├── reciprocity
│ ├── overall_reciprocity
│ └── reciprocity
├── regular
│ ├── is_k_regular
│ └── is_regular
├── shortest_paths
│ ├── dense
│ │ ├── floyd_warshall
│ │ ├── floyd_warshall_numpy
│ │ └── floyd_warshall_predecessor_and_distance
│ ├── generic
│ │ └── has_path
│ ├── unweighted
│ │ ├── all_pairs_shortest_path_length
│ │ ├── single_source_shortest_path_length
│ │ └── single_target_shortest_path_length
│ └── weighted
│ ├── all_pairs_bellman_ford_path_length
│ ├── bellman_ford_path
│ ├── bellman_ford_path_length
│ ├── negative_edge_cycle
│ └── single_source_bellman_ford_path_length
├── simple_paths
│ └── is_simple_path
├── smetric
│ └── s_metric
├── structuralholes
│ └── mutual_weight
├── tournament
│ ├── is_tournament
│ ├── score_sequence
│ └── tournament_matrix
├── traversal
│ └── breadth_first_search
│ ├── bfs_layers
│ └── descendants_at_distance
└── triads
└── is_triad
项目详情
下载文件
下载您平台的文件。如果您不确定选择哪个,请了解更多关于 安装软件包 的信息。
源分发
构建分发
graphblas-algorithms-2023.10.0.tar.gz 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 059be9faaef2697a1d29e4fd50ae11a6ee6d91bb6c1c341f6138121aca4b40f4 |
|
| MD5 | 4efcc0c4e09419a2bf9934d14e4d2e4f |
|
| BLAKE2b-256 | 0b4899579d5bfc2f6a9f8b30dac947c00a41eb9a410d04605c66f0e2bc9bae73 |
graphblas_algorithms-2023.10.0-py3-none-any.whl 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 75f135a756c4a3a52796a5967d0c9131af03596937c2f918cba6d9b714666fa3 |
|
| MD5 | 7fd71eac02dd65545e85fdc21ab008cc |
|
| BLAKE2b-256 | fcd7c98979217e0bc3fb066601eba26c75ec865b9560a4700a99c1cb87fe4dc4 |