通用粒子+网格接口
项目描述
GPGI
后处理时间快速粒子沉积
这个小Python库实现了基本的网格沉积算法,用于分析(矩形)网格+粒子数据集,重点在于性能。核心算法作为Cython扩展实现。
GPGI代表 通用 粒子 + 网格 数据 接口
目录
安装
python -m pip install --upgrade pip
python -m pip install gpgi
支持的应用程序
矩形网格定义为每个方向上表示单元格左边缘的1D数组。请注意,这种数组的最后一个点被解释为最右单元格的右边缘,因此,例如,包含100个单元格的1D网格由101个边缘定义。
粒子定义为存在于网格边界内的点。
沉积是从粒子描述到字段网格描述的动作。在分析、比较和组合存在于两种形式结合的模拟数据时非常有用。这个过程是不可逆的,因为它会降低信息。
例如,下面是一个粒子集(红色点)与表示沉积粒子计数的背景的简单叠加。
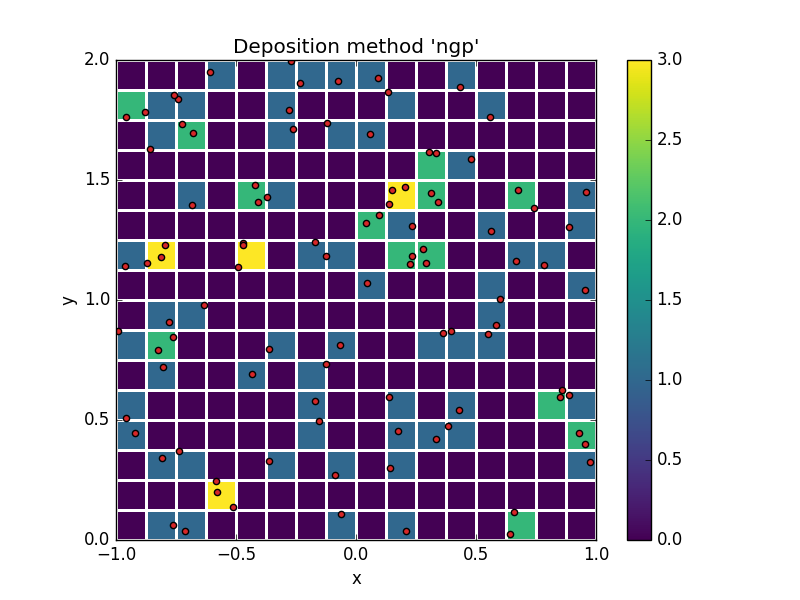
此示例说明了最简单的沉积方法“最近网格点”(NGP),其中每个粒子仅对其包含的单元格做出贡献。
还有更多精细的方法可供选择。
内置沉积方法
| 方法名称 | 缩写名称 | 顺序 |
|---|---|---|
| 最近网格点 | NGP | 0 |
| 单元格中的云 | CIC | 1 |
| 三角形形状的云 | TSC | 2 |
gpgi 0.12 新增 可以通过 method=my_func 将用户定义的替代方法提供到 Dataset.deposit 中。它们的签名需要与 gpgi.types.DepositionMethodT 兼容。
支持的几何形状
| 几何名称 | 坐标轴顺序 |
|---|---|
| 笛卡尔 | x, y, z |
| 极坐标 | 半径, z, 方位角 |
| 柱坐标 | 半径, 方位角, z |
| 球坐标 | 半径, 纬度, 方位角 |
| 赤道 | 半径, 方位角, 纬度 |
时间复杂度
沉积过程中一个重要的步骤是将粒子索引与单元格索引关联起来。这个步骤称为“粒子索引”。在网格均匀步进的方向上(如果有),索引粒子的操作是 O(1) 操作。在更一般的情况下,索引是通过二分法进行的,这是一个 O(log(nx))) 操作(其中 nx 代表感兴趣方向上的单元格数量)。
用法
API 由一个返回 Dataset 对象的 load 函数组成。
加载数据
import numpy as np
import gpgi
nx = ny = 64
nparticles = 600_000
prng = np.random.RandomState(0)
ds = gpgi.load(
geometry="cartesian",
grid={
"cell_edges": {
"x": np.linspace(-1, 1, nx),
"y": np.linspace(-1, 1, ny),
},
},
particles={
"coordinates": {
"x": 2 * (prng.normal(0.5, 0.25, nparticles) % 1 - 0.5),
"y": 2 * (prng.normal(0.5, 0.25, nparticles) % 1 - 0.5),
},
"fields": {
"mass": np.ones(nparticles),
},
},
)
Dataset 对象包含一个 grid 和一个 particles 属性,它们都包含一个 fields 属性,用于访问它们的数据。但更重要的是,Dataset 有一个 deposit 方法可以将粒子场转换为网格形式。
将粒子场沉积到网格上
particle_mass = ds.deposit("mass", method="nearest_grid_point") # or "ngp" for shorts
可视化 在此示例中,我们将使用 matplotlib 进行渲染,但请注意,matplotlib 不是 gpgi 的依赖项。
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.set(aspect=1, xlabel="x", ylabel="y")
im = ax.pcolormesh(
"x",
"y",
particle_mass.T,
data=ds.grid.cell_edges,
cmap="viridis",
)
fig.colorbar(im, ax=ax)
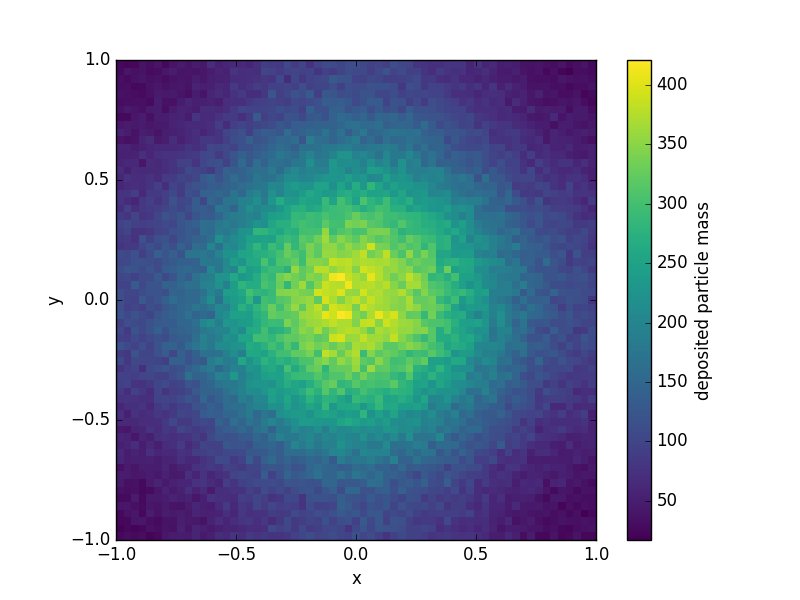
这里给出的示例脚本大约需要一秒钟(从上到下)。
提供任意元数据
gpgi 0.4.0 新增
Dataset 对象有一个特殊的 metadata 属性,它是一个具有字符串键的字典。这个属性旨在保存任何可能与标记或处理相关的特殊元数据(例如,模拟时间、作者等)。元数据可以在加载数据时提供。
ds = gpgi.load(
geometry="cartesian",
grid=...,
particles=...,
metadata={"simulation_time": 12.5, "author": "Clément Robert"}
)
边界条件
gpgi 0.5.0 新增
CIC 和 TSC 沉积中,粒子会对包含它们的单元格相邻的单元格做出贡献。对于位于域最外层层的粒子,这意味着它们的一些贡献会丢失。这种行为对应于默认的 'open' 边界条件,但 gpgi 内置了对更保守边界条件的支持。
可以根据字段、坐标轴和侧面选择边界条件。内置的配方都是执行幽灵层(同一侧和相对侧)和活动域层(同一侧和相对侧)的线性组合,并用结果替换同一侧的活动层。
用户选择的边界条件是 Dataset.deposit 的一个可选参数,形式为字典,键是坐标轴名称,值是边界条件名称的 2 元组(分别对应左右两侧)。例如,以下是要求所有轴上都具有周期性边界条件的示例:
ds.deposit(
"mass",
method="cic",
boundaries={
"x": ("periodic", "periodic"),
"y": ("periodic", "periodic"),
}
)
未指定的轴将使用默认的 'open' 边界。
内置食谱
| 边界条件 | 描述 | 保守? |
|---|---|---|
| 打开(默认) | 无特殊处理 | 无 |
| 周期性 | 向活动域添加相对幽灵层 | 是 |
| 墙 | 向活动域添加同一侧幽灵层 | 是 |
| 反对称 | 从活动域中减去同一侧幽灵层 | 无 |
定义自定义食谱
gpgi 的边界配方可以进行自定义。让我们用一个简单的例子来说明这个特性。假设我们想固定沉积字段在外层中的值。这是通过在用户端定义一个新函数来实现的
def ones(
same_side_active_layer,
same_side_ghost_layer,
opposite_side_active_layer,
opposite_side_ghost_layer,
weight_same_side_active_layer,
weight_same_side_ghost_layer,
weight_opposite_side_active_layer,
weight_opposite_side_ghost_layer,
side,
metadata,
):
return 1.0
其中前八个参数都是形状相同的 numpy.ndarray 对象(包括幽灵填充!),返回值必须可以广播到这些对象,side 只能是 "left" 或 "right",而 metadata 是特殊的 Dataset.metadata 属性。并非必须使用函数体内的所有参数,但需要这个签名。
然后必须将这个方法注册为边界条件配方,如下所示
ds.boundary_recipes.register("ones", ones)
其中关联的键(在这里是 "ones")是任意的。配方现在可以使用得与内置配方完全一样,并且可以任意混合使用。
ds.deposit(
"mass",
method="cic",
boundaries={
"x": ("ones", "wall"),
"y": ("periodic", "periodic"),
}
)
请注意,边界配方函数中的前八个参数应代表一个广度物理量(与强度相对)。当沉积一个强度量u时,应提供一个权重字段w(参见下一节),在这种情况下,前四个参数表示u*w,接下来的四个参数表示w,这样u就可以在函数中作为比例来获得,如果需要的话。
权重字段(沉积密集量)
自gpgi 0.7.0版引入
从根本上讲,沉积算法通过执行求和来构建网格上的场。这意味着正在沉积的物理量必须是广度的(如质量或动量)。强度量(如速度或温度)需要额外的操作,并需要使用额外的权重字段。
本节展示了它们的使用示例。有关强度量沉积算法的详细说明,请参阅沉积算法。
为了沉积一个强度场(例如,vx),必须提供额外的weight_field参数。
ds.deposit(
"vx",
method="cic",
boundaries={
"y": ("periodic", "periodic"),
"x": ("antisymmetric", "antisymmetric"),
},
weight_field="mass",
weight_field_boundaries={
"y": ("periodic", "periodic"),
"x": ("open", "open"),
},
)
边界配方还可以与权重字段相关联,使用weight_field_boundaries参数。如果同时提供了boundaries和weight_field,则此参数变为必需。
调用help(ds.deposit)获取更多详细信息。
计数排序
自gpgi 0.14.0版引入
gpgi可以加载任意顺序的粒子集,尽管当内存中粒子的位置与它们相对于网格的物理位置相关联时,沉积算法的性能会更好,因为这种状态可以最小化缓存未命中次数。
可以使用计数排序算法对粒子进行排序,如下所示
ds = ds.sorted()
请注意,此方法返回数据集的副本,因此它最适合那些最多只能占用你一半RAM的数据集。
此操作本身成本较高,因此根据在丢弃数据集之前需要在数据集上执行多少次沉积,可能会有权衡。
默认情况下,轴的权重顺序对gpgi的沉积例程来说是最优的,但也可以指定任意的优先级顺序,例如
ds = ds.sorted(axes=(1, 0))
使用Dataset.is_sorted方法检查粒子是否已经排序,而不执行排序。Dataset.is_sorted接受一个与Dataset.sorted相同的axes参数。这对于测试和比较目的很有用。
沉积算法
本节提供了关于在gpgi中实现的通用沉积算法的详细说明。
不失一般性,我们将说明如何沉积一个强度场(v),因为这种情况需要最多的计算步骤。事实上,单独沉积一个广度场(w)实际上是算法的一部分。
定义
v是我们想要沉积到网格上的一个强度场w是一个用作权重的广度场u = v * w是v的广度等效物(概念上,如果v是速度,而w是质量,则u对应于动量)
u(i)、v(i)和w(i)为每个粒子i定义。
我们记U(x)、V(x)和W(x)为相应的网格场,其中V(x)是算法的最终输出。这些定义在网格单元中心x,在活动域内。
最后,我们记U'(x)、V'(x)和W'(x)为原始沉积场,这意味着没有对最外层(边界条件)应用特殊处理。这些定义在网格单元中心,包括一个用于应用边界条件的鬼层。
算法
W'和U'的计算方法如下
W'(x) = Σ c(i,x) w(i)
U'(x) = Σ c(i,x) w(i) v(i)
其中,c(i,x) 是与沉积方法相关的几何系数。以最近网格点(NGP)方法为例,如果粒子 i 包含在中心为 x 的单元格中,则 c(i,x) = 1;否则 c(i,x) = 0。
- 应用边界条件
W(x) = W_BCO(W', 1, metadata)
U(x) = U_BCO(U', W', metadata)
其中,W_BCO 和 U_BCO 分别表示与 W 和 U 相关的任意边界条件算子,它们接受 3 个参数,代表要转换的场、相关权重场和一个通配符 metadata 参数,该参数可能包含与算子相关的任何其他数据。
注意,1 被用作 W 的“权重”占位符,出于对称性原因:所有边界条件算子都必须公开类似的接口,如定义自定义配方中所述。
- 最后,
V(x)通过以下方式获得
V(x) = (U/W)(x)
项目详情
下载文件
下载您平台的文件。如果您不确定选择哪个,请了解更多关于 安装包 的信息。
源分布
构建分布
哈希值 for gpgi-1.0.0-cp312-cp312-musllinux_1_1_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 1460cb78bf953db0a883128d94a87024eca22c1233aaa95cacc20ba6983d671b |
|
| MD5 | d9b4c29e97ca7f7b5a1bc6c706b95141 |
|
| BLAKE2b-256 | a786313b3b197edf138f6e27e195d46fb7c98a63676072cd72079274c5be4fc3 |
哈希值 for gpgi-1.0.0-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 0e6c6e742e197f4b539b9d5ba2ff3e701e658da73e310272b4ba95f4e18a9575 |
|
| MD5 | 900c575c2f04637649ff72da8ad87189 |
|
| BLAKE2b-256 | e2ecaa09a7eb3f5bbe688ed884476f09da259525dd6d15aeb3f73079b7b9e680 |
哈希值 for gpgi-1.0.0-cp312-cp312-macosx_10_9_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 812a2a84e3bd7d7619fefc95d52a808ab48422de51e64a1cc52a947ba621319c |
|
| MD5 | d47cd78697750d679a98b6a78f9cc8a8 |
|
| BLAKE2b-256 | 862fadff2386544a532698a0aecd91e2b8138ae6c33221f2d1277eb84440091a |
哈希值 for gpgi-1.0.0-cp311-cp311-musllinux_1_1_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | e3eaf3aa8a92b242c271bf1c629b310cf47162a2538031fac64040a4e473ffe6 |
|
| MD5 | ee81778f6806f682d9490e11f23e46aa |
|
| BLAKE2b-256 | 1a9ecdf57a726bdddc4cebbf652a3f769a726f46f874af4c5c19444c5187b977 |
哈希值 for gpgi-1.0.0-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | b673a4ab6143bacbb66656f35588625ca23ba3c11c54b06421017195310b8b6a |
|
| MD5 | 4e1bef70489ade0926bdb818ffb61e4b |
|
| BLAKE2b-256 | 07bac4440bac60fa30115f87d545a47f23bbf4a861af06e8a1dd7c8cc1311272 |
哈希值 for gpgi-1.0.0-cp311-cp311-macosx_10_9_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | d5d10300a59f924eced43eacc981b19654a628dc271647f988d35946d8077025 |
|
| MD5 | 217ef1e5dc8337e459d7581e681b0365 |
|
| BLAKE2b-256 | 9afdc60080d711ad6695b5c5dafa916d11e0bc5610368c467f985c6363f8f9cf |
哈希值 for gpgi-1.0.0-cp310-cp310-musllinux_1_1_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 27c1ef9bd574741074af90249f568aabcf7ddadc022cc47425d688215a24569d |
|
| MD5 | a1bd6d114ac637e8ea2cf8d203585967 |
|
| BLAKE2b-256 | e7a5c7f935f5b716dd135dcc11797adb820f40e383f06164bace8bcdc0f3673f |
哈希值 用于 gpgi-1.0.0-cp310-cp310-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 1b46b57ca74ad95601222b96904a4cc000ff345d27ab477b23ab921a89341ed3 |
|
| MD5 | c16f531462b9a1f547cf671eb16c0e73 |
|
| BLAKE2b-256 | 005b0750248ce8d0fa14b75afcdd7b530129410a9309c68d93f5c586a572b91f |
哈希值 用于 gpgi-1.0.0-cp310-cp310-macosx_10_9_x86_64.whl
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 5da1885b3711f545949f9e6de3059b18cd1ab69fb711823f036f147a3219abef |
|
| MD5 | 731d644a9dd4bfb08952aeee5583ac20 |
|
| BLAKE2b-256 | ec74c0333764e95281098cb66601d7e7e884119fd1178bf243b211c0ec22b822 |






