深度连续分位数回归
项目描述
深度连续分位数回归
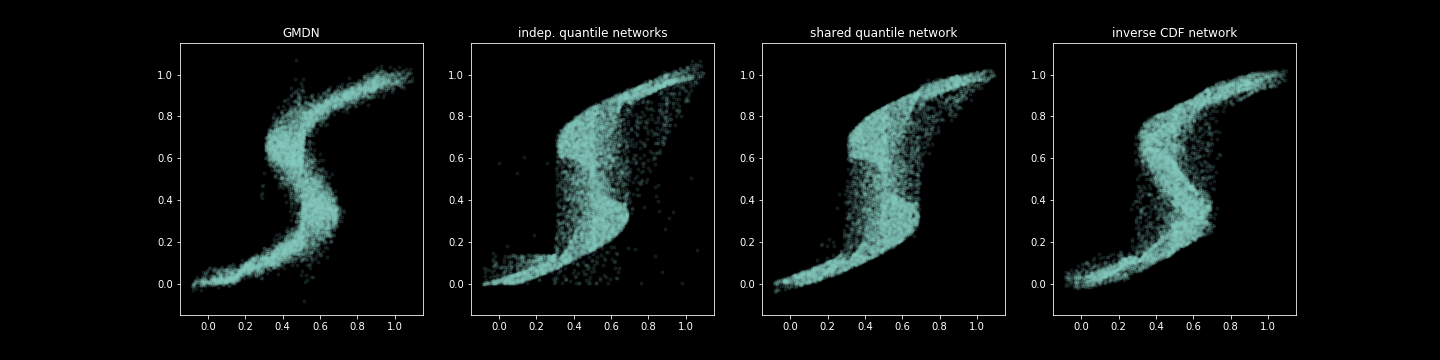
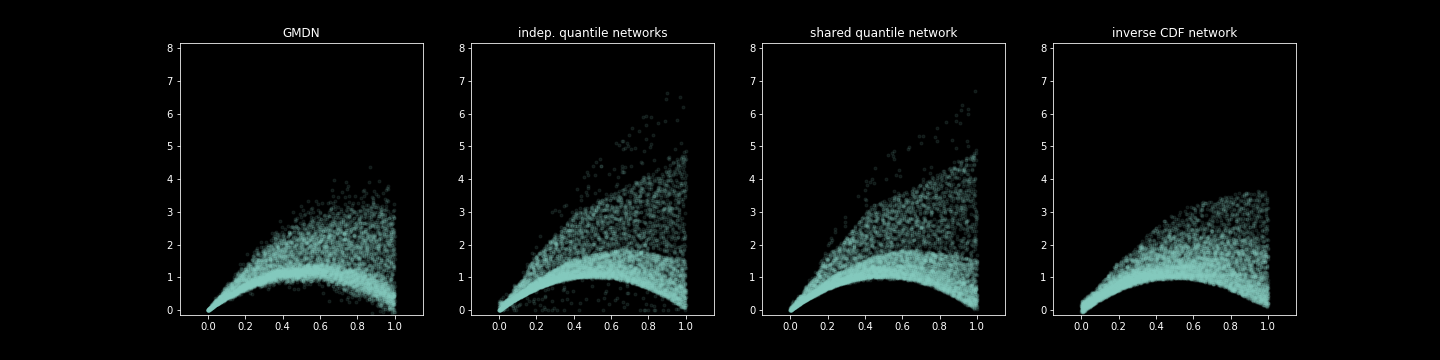
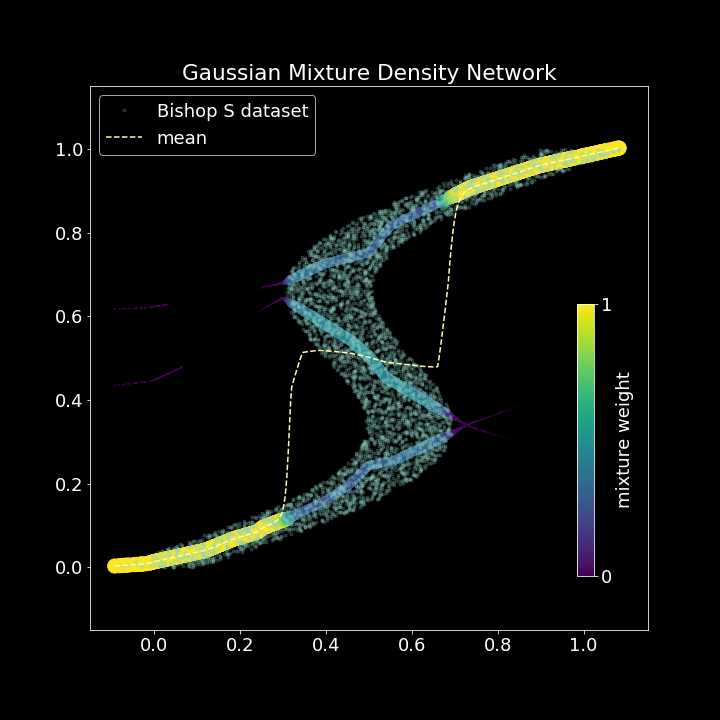
本包探讨了学习目标变量不确定性的不同方法,更一般地,学习条件分布。我们引入了一种新的网络类型,即“深度连续分位数回归网络”,它通过多层感知器直接近似条件逆条件累积分布函数,而不是依赖于需要关于分布函数形式的先验知识的变分方法。在许多情况下,我们发现它是对著名的混合密度网络的一个稳健的替代方案。
这尤其重要当
- 目标变量的均值对于用例来说不够用时
- 误差是异方差性的,即根据输入特征变化
- 误差是偏斜的,使得如方差这样的单个汇总统计量不充分。
我们探索两种主要方法
- 拟合混合密度模型
- 学习分布的条件分位数的位置,
q。
我们的混合密度网络利用了一种实现技巧,在keras中实现负对数似然最小化。
相同的技巧用于优化分位数回归网络中的“pinball”损失,并且事实上可以用于优化任意损失函数(X, y, y_hat)。
在基于分位数的范围内,我们进一步探索:a. 对每个分位数拟合一个单独的模型进行预测 b. 拟合一个多输出网络同时预测多个分位数 c. 同时在X和q上进行回归学习,从而有效地学习完整的(条件)累积分布函数。
安装
从源安装包
pip install git+https://github.com/ig248/deepquantiles
或从PyPi安装
pip install deepquantiles
使用方法
from deepquantiles import MultiQuantileRegressor, InverseCDFRegressor, MixtureDensityRegressor
由于这个包很大程度上是一个实验,请探索Jupyter笔记本,并期待查看源代码。
内容
deepqunatiles.regressors:核心算法的实现deepquantiles.presets:实验中使用的预配置估计量和设置集合deepquantiles.datasets:用于生成测试数据的函数deepquantiles.nb_utils:用于笔记本的辅助函数notebooks:包含示例和实验的Jupyter笔记本
测试
运行
make dev-install
make lint
make test
参考文献
混合密度网络,Christopher M. Bishop,NCRG/94/004 (1994)
项目详情
关闭
deepquantiles-0.0.2.tar.gz的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 91023eec0c9745f34b0fa558b4090aceac4fbe3454836f7c3d45e55ae0dbb0fa |
|
| MD5 | 49a0bd35b040d95e485ff8ac1267945d |
|
| BLAKE2b-256 | e17349fb5e90c7176393690020fb2a3d9b4b852ea451ff850fa49855c00ae8e0 |
关闭
deepquantiles-0.0.2-py2.py3-none-any.whl的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | a80aa4a121cf23477f8d235a8fcfe0ddb6ae664b21baed5b37315b5f9413aed7 |
|
| MD5 | 109ad89698838a67d1de51c37ad846fe |
|
| BLAKE2b-256 | ec44954fb3dcdde500d3b7ab7cae302c11d36179ff9d116a88d5c8178e8f38ad |