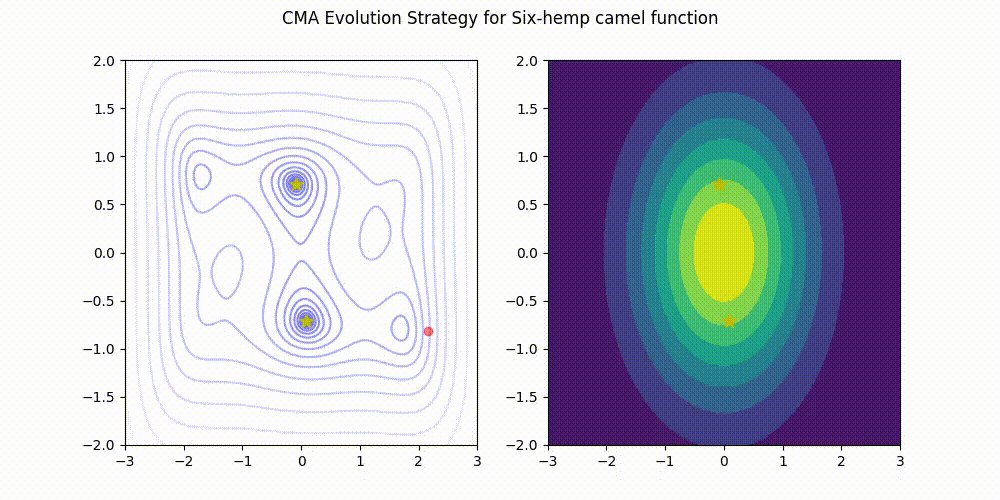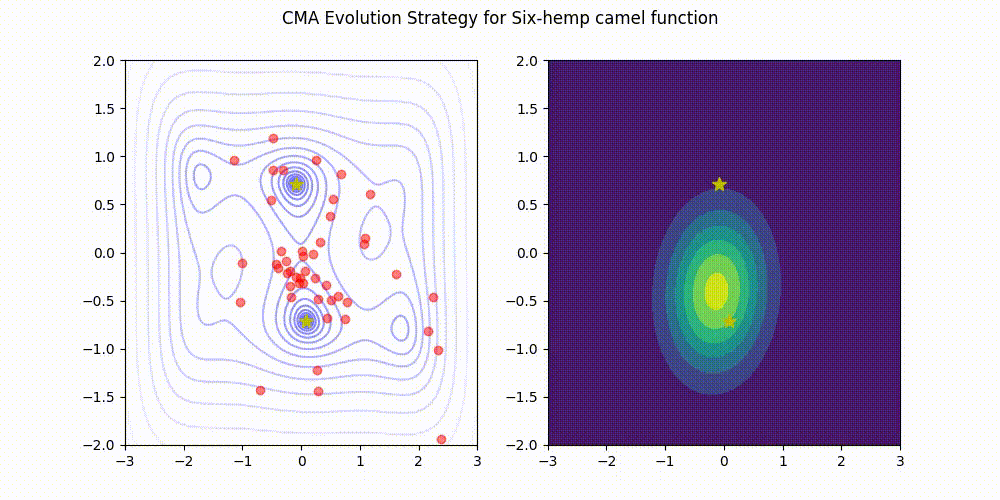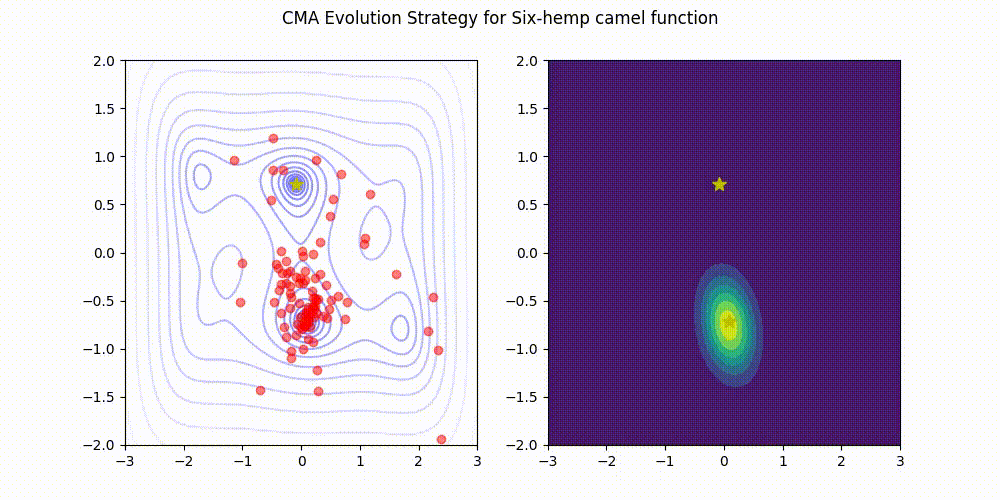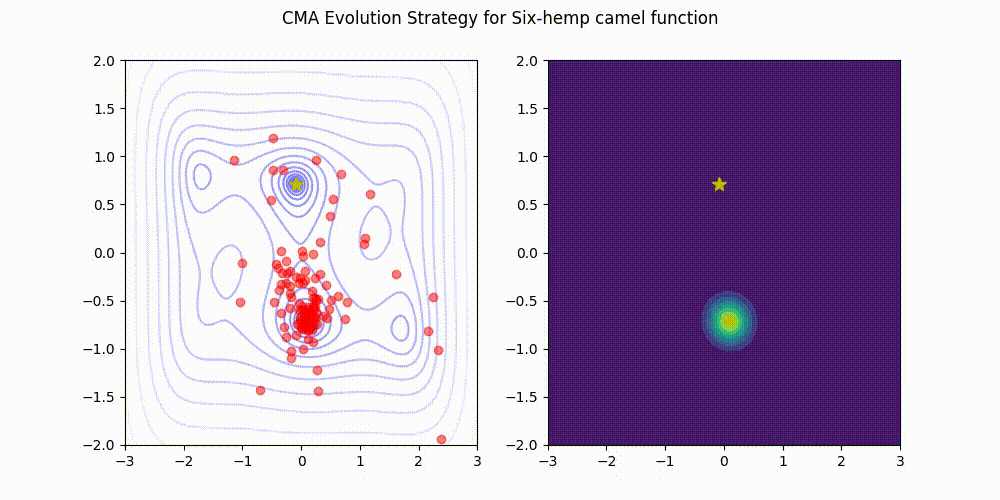
为Python 3实现的轻量级协方差矩阵自适应进化策略(CMA-ES)。
项目描述
cmaes
:whale: 论文现在可在arXiv上找到!
简单且实用的CMA-ES Python库。请参阅论文 [Nomura and Shibata 2024] 以获取详细信息,包括设计理念和高级示例。
安装
支持的Python版本为3.7或更高。
$ pip install cmaes
或者您可以通过conda-forge安装。
$ conda install -c conda-forge cmaes
使用方法
此库提供了一个“询问并告知”风格的接口。我们采用CMA-ES的标准版本[Hansen 2016]。
import numpy as np
from cmaes import CMA
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
if __name__ == "__main__":
optimizer = CMA(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
您可以通过Optuna [Akiba et al. 2019],一个自动超参数优化框架来使用这个库。Optuna 内置的 CMA-ES 样本器,在底层使用此库,从v1.3.0版本开始提供,并在v2.0.0版本中稳定。有关更多详细信息,请参阅文档或v2.0 发布博客。
import optuna
def objective(trial: optuna.Trial):
x1 = trial.suggest_uniform("x1", -4, 4)
x2 = trial.suggest_uniform("x2", -4, 4)
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
if __name__ == "__main__":
sampler = optuna.samplers.CmaEsSampler()
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=250)
CMA-ES 变体
学习率自适应 CMA-ES [Nomura et al. 2023]
CMA-ES 在面对诸如多模态或噪声等困难问题时,如果其超参数值未正确配置,其性能可能会下降。学习率自适应 CMA-ES(LRA-CMA)通过自动调整学习率有效地解决了这个问题,因此 LRA-CMA 消除了昂贵超参数调整的需要。
只需在 CMA() 的初始化中添加 lr_adapt=True 即可使用 LRA-CMA。
源代码
import numpy as np
from cmaes import CMA
def rastrigin(x):
dim = len(x)
return 10 * dim + sum(x**2 - 10 * np.cos(2 * np.pi * x))
if __name__ == "__main__":
dim = 40
optimizer = CMA(mean=3*np.ones(dim), sigma=2.0, lr_adapt=True)
for generation in range(50000):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = rastrigin(x)
if generation % 500 == 0:
print(f"#{generation} {value}")
solutions.append((x, value))
optimizer.tell(solutions)
if optimizer.should_stop():
break
完整的源代码可在此处找到。
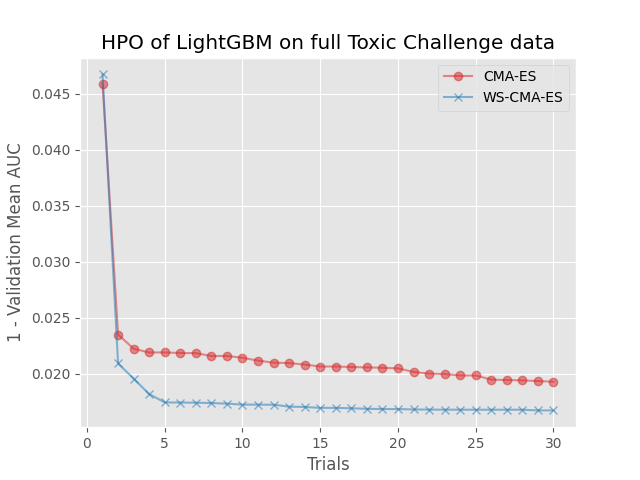
热启动 CMA-ES [Nomura et al. 2021]
热启动 CMA-ES(WS-CMA)是一种通过 CMA-ES 的初始化转移相似任务的前知识的方法。这在评估预算有限(例如,机器学习算法的超参数优化)时特别有用。
源代码
import numpy as np
from cmaes import CMA, get_warm_start_mgd
def source_task(x1: float, x2: float) -> float:
b = 0.4
return (x1 - b) ** 2 + (x2 - b) ** 2
def target_task(x1: float, x2: float) -> float:
b = 0.6
return (x1 - b) ** 2 + (x2 - b) ** 2
if __name__ == "__main__":
# Generate solutions from a source task
source_solutions = []
for _ in range(1000):
x = np.random.random(2)
value = source_task(x[0], x[1])
source_solutions.append((x, value))
# Estimate a promising distribution of the source task,
# then generate parameters of the multivariate gaussian distribution.
ws_mean, ws_sigma, ws_cov = get_warm_start_mgd(
source_solutions, gamma=0.1, alpha=0.1
)
optimizer = CMA(mean=ws_mean, sigma=ws_sigma, cov=ws_cov)
# Run WS-CMA-ES
print(" g f(x1,x2) x1 x2 ")
print("=== ========== ====== ======")
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = target_task(x[0], x[1])
solutions.append((x, value))
print(
f"{optimizer.generation:3d} {value:10.5f}"
f" {x[0]:6.2f} {x[1]:6.2f}"
)
optimizer.tell(solutions)
if optimizer.should_stop():
break
完整的源代码可在此处找到。
带边界的 CMA-ES [Hamano et al. 2022]
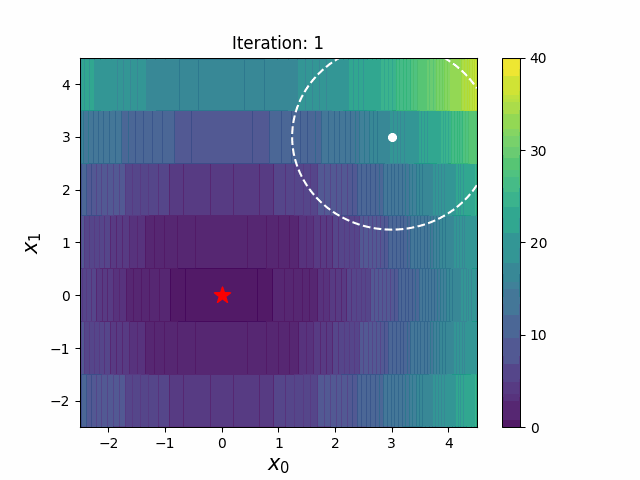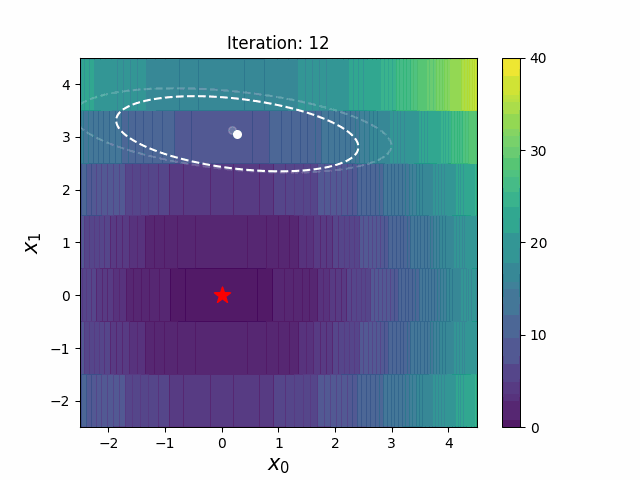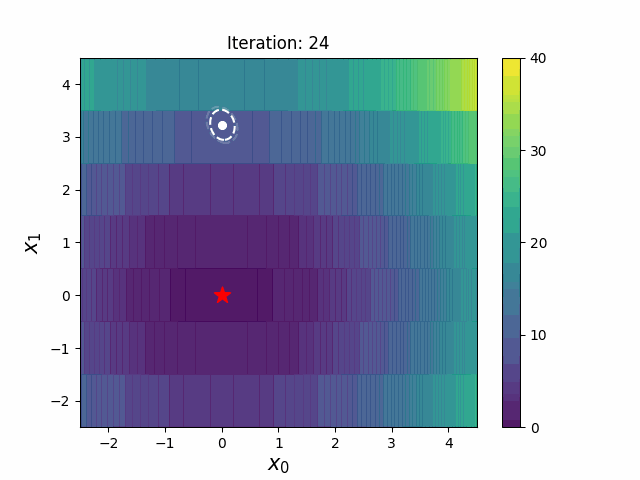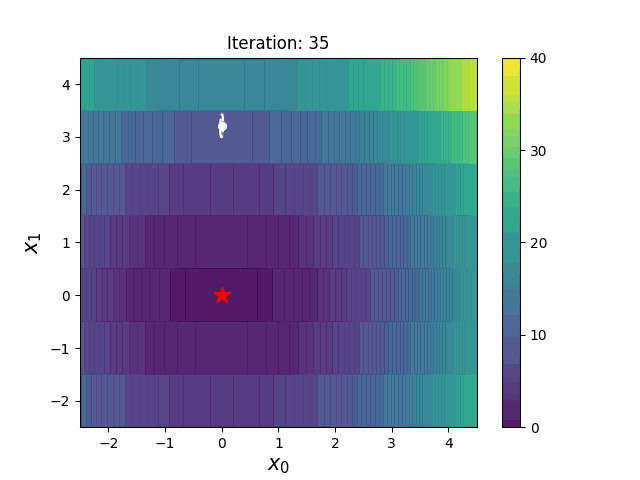
带边界的 CMA-ES(CMAwM)为每个离散维度引入了边际概率的下限,确保样本不会固定在单一点。此方法可以应用于由连续(如浮点)和离散元素(包括整数和二进制类型)组成的混合空间。
| CMA | CMAwM |
|---|---|
 |
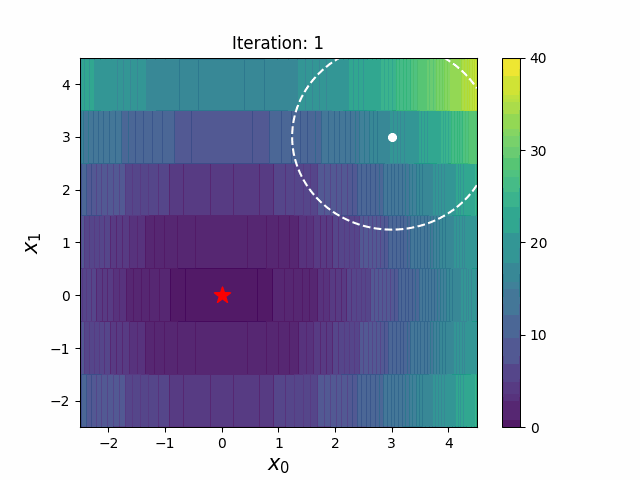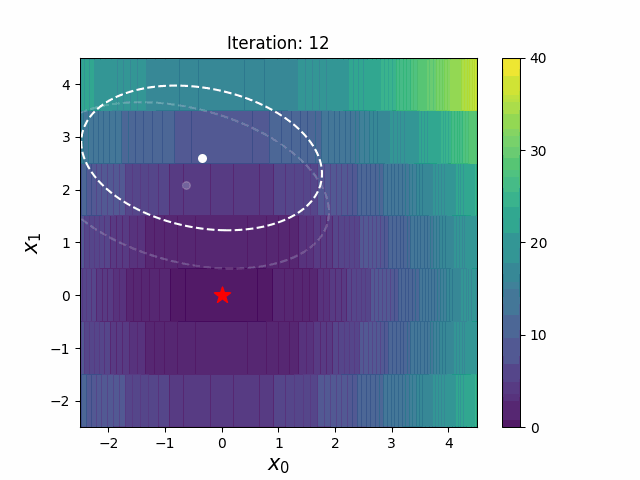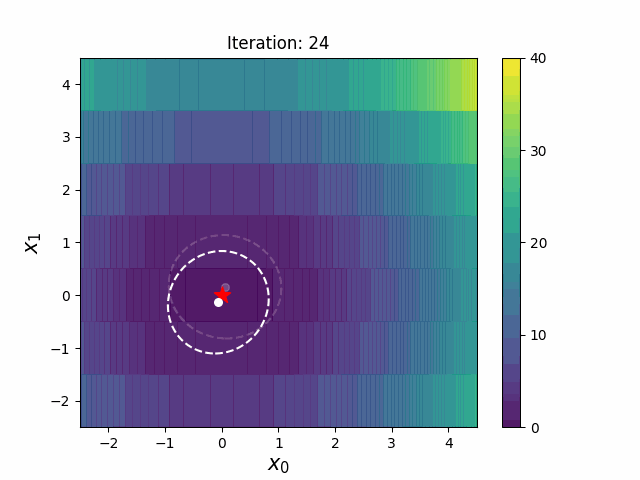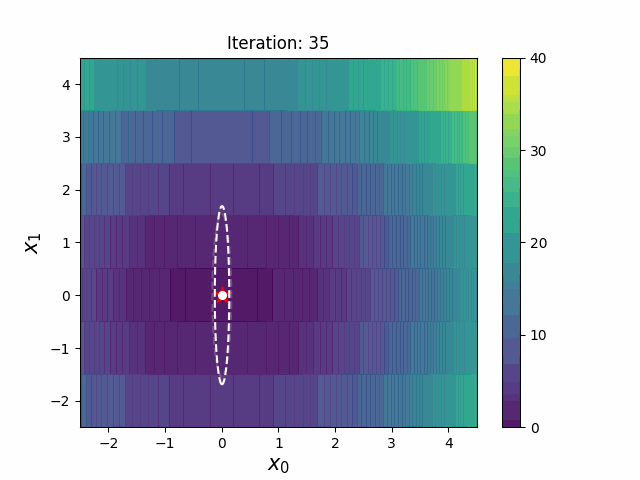 |
以上图表来自EvoConJP/CMA-ES_with_Margin。
源代码
import numpy as np
from cmaes import CMAwM
def ellipsoid_onemax(x, n_zdim):
n = len(x)
n_rdim = n - n_zdim
r = 10
if len(x) < 2:
raise ValueError("dimension must be greater one")
ellipsoid = sum([(1000 ** (i / (n_rdim - 1)) * x[i]) ** 2 for i in range(n_rdim)])
onemax = n_zdim - (0.0 < x[(n - n_zdim) :]).sum()
return ellipsoid + r * onemax
def main():
binary_dim, continuous_dim = 10, 10
dim = binary_dim + continuous_dim
bounds = np.concatenate(
[
np.tile([-np.inf, np.inf], (continuous_dim, 1)),
np.tile([0, 1], (binary_dim, 1)),
]
)
steps = np.concatenate([np.zeros(continuous_dim), np.ones(binary_dim)])
optimizer = CMAwM(mean=np.zeros(dim), sigma=2.0, bounds=bounds, steps=steps)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = ellipsoid_onemax(x_for_eval, binary_dim)
evals += 1
solutions.append((x_for_tell, value))
if evals % 300 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
源代码也在此处提供。
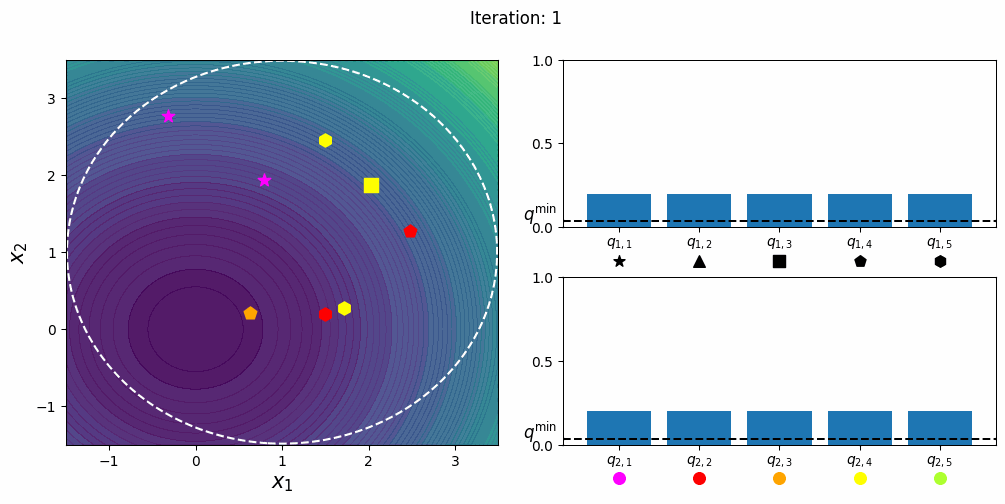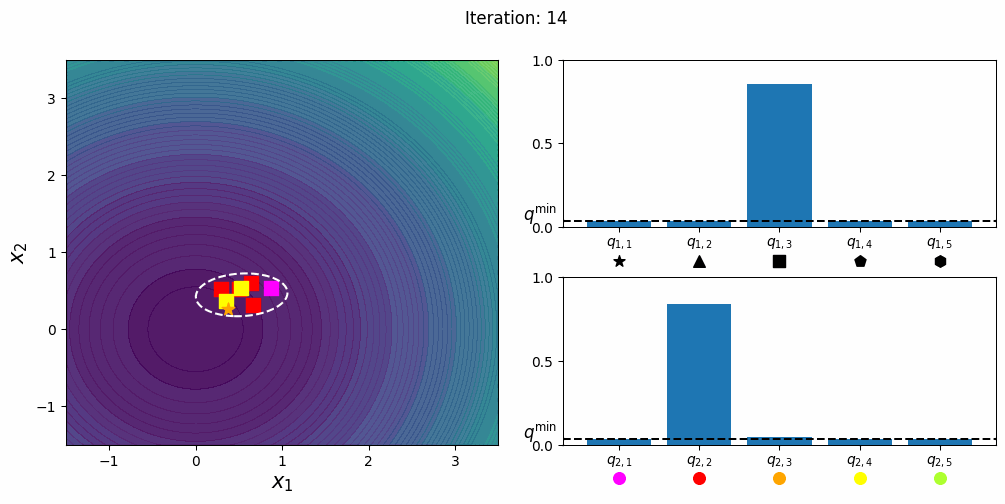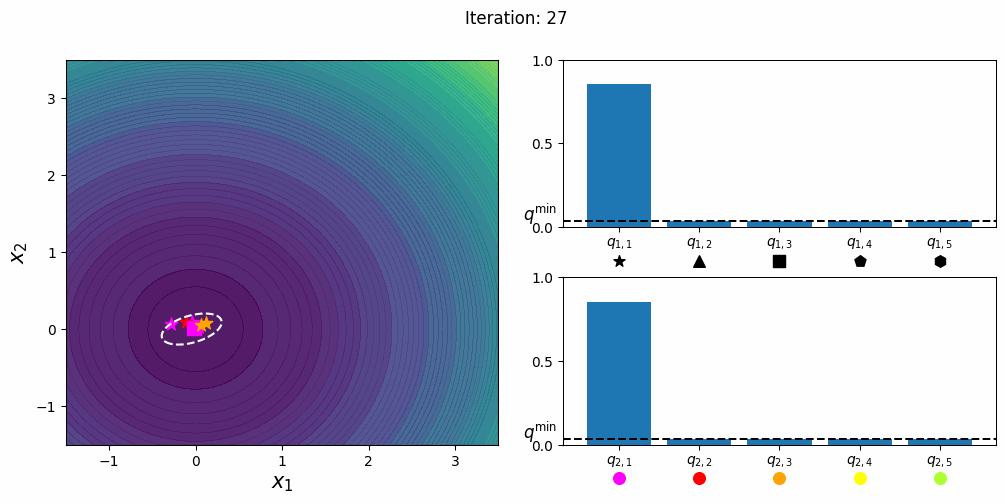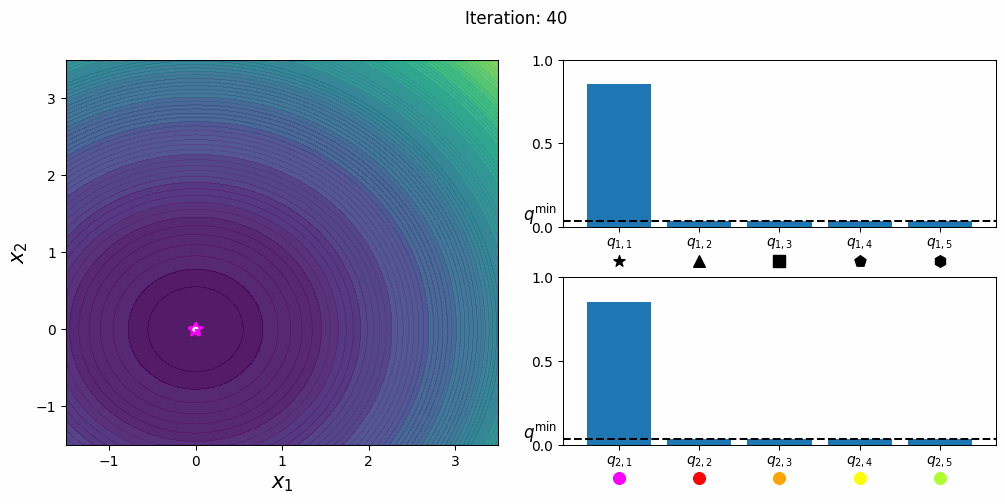
CatCMA [Hamano et al. 2024]
CatCMA 是一种用于混合类别优化问题的方法,即同时优化连续和类别变量的问题。CatCMA 使用多元高斯分布和类别分布的联合概率分布作为搜索分布。
源代码
import numpy as np
from cmaes import CatCMA
def sphere_com(x, c):
dim_co = len(x)
dim_ca = len(c)
if dim_co < 2:
raise ValueError("dimension must be greater one")
sphere = sum(x * x)
com = dim_ca - sum(c[:, 0])
return sphere + com
def rosenbrock_clo(x, c):
dim_co = len(x)
dim_ca = len(c)
if dim_co < 2:
raise ValueError("dimension must be greater one")
rosenbrock = sum(100 * (x[:-1] ** 2 - x[1:]) ** 2 + (x[:-1] - 1) ** 2)
clo = dim_ca - (c[:, 0].argmin() + c[:, 0].prod() * dim_ca)
return rosenbrock + clo
def mc_proximity(x, c, cat_num):
dim_co = len(x)
dim_ca = len(c)
if dim_co < 2:
raise ValueError("dimension must be greater one")
if dim_co != dim_ca:
raise ValueError(
"number of dimensions of continuous and categorical variables "
"must be equal in mc_proximity"
)
c_index = np.argmax(c, axis=1) / cat_num
return sum((x - c_index) ** 2) + sum(c_index)
if __name__ == "__main__":
cont_dim = 5
cat_dim = 5
cat_num = np.array([3, 4, 5, 5, 5])
# cat_num = 3 * np.ones(cat_dim, dtype=np.int64)
optimizer = CatCMA(mean=3.0 * np.ones(cont_dim), sigma=1.0, cat_num=cat_num)
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x, c = optimizer.ask()
value = mc_proximity(x, c, cat_num)
if generation % 10 == 0:
print(f"#{generation} {value}")
solutions.append(((x, c), value))
optimizer.tell(solutions)
if optimizer.should_stop():
break
完整的源代码可在此处找到。
可分离 CMA-ES [Ros and Hansen 2008]
可分离 CMA-ES(Sep-CMA-ES)是一种将协方差矩阵限制为对角形式算法。这种参数数量的减少增强了可扩展性,使得 Sep-CMA-ES 非常适合高维优化任务。此外,协方差矩阵的学习率也得到了提高,这使得 Sep-CMA-ES 在可分离函数上比(全协方差)CMA-ES 有更好的性能。
源代码
import numpy as np
from cmaes import SepCMA
def ellipsoid(x):
n = len(x)
if len(x) < 2:
raise ValueError("dimension must be greater one")
return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])
if __name__ == "__main__":
dim = 40
optimizer = SepCMA(mean=3 * np.ones(dim), sigma=2.0)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ellipsoid(x)
evals += 1
solutions.append((x, value))
if evals % 3000 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
完整的源代码可在此处找到。
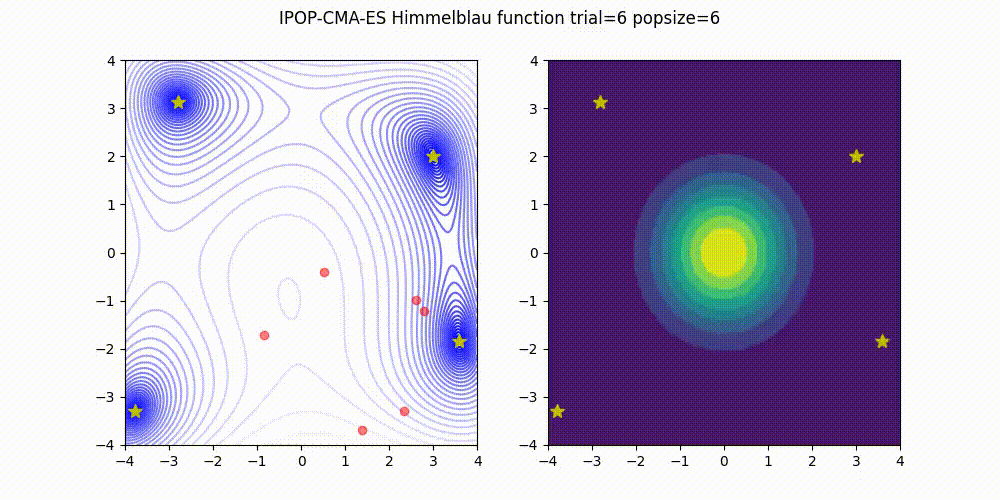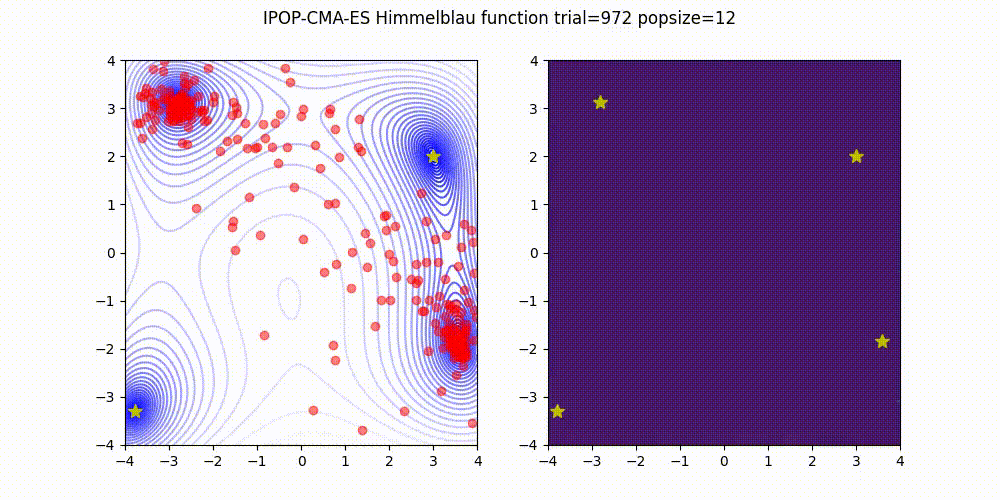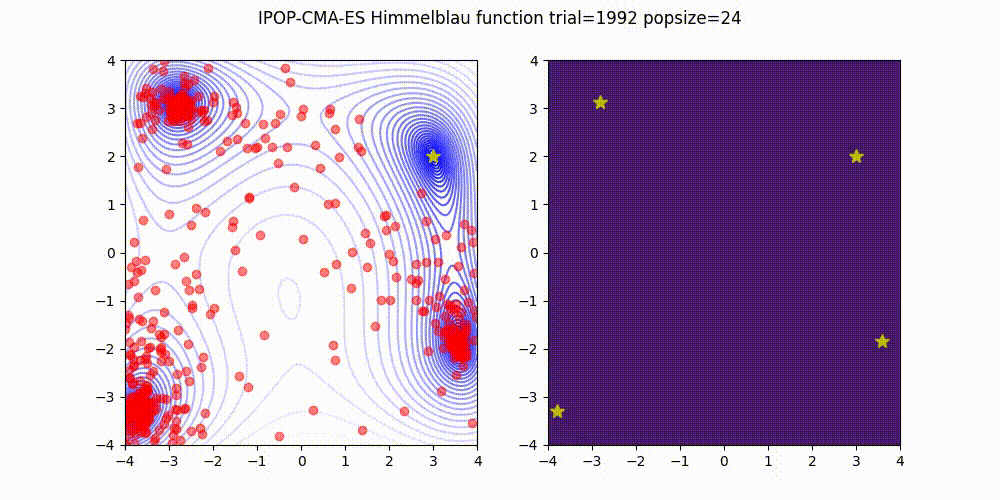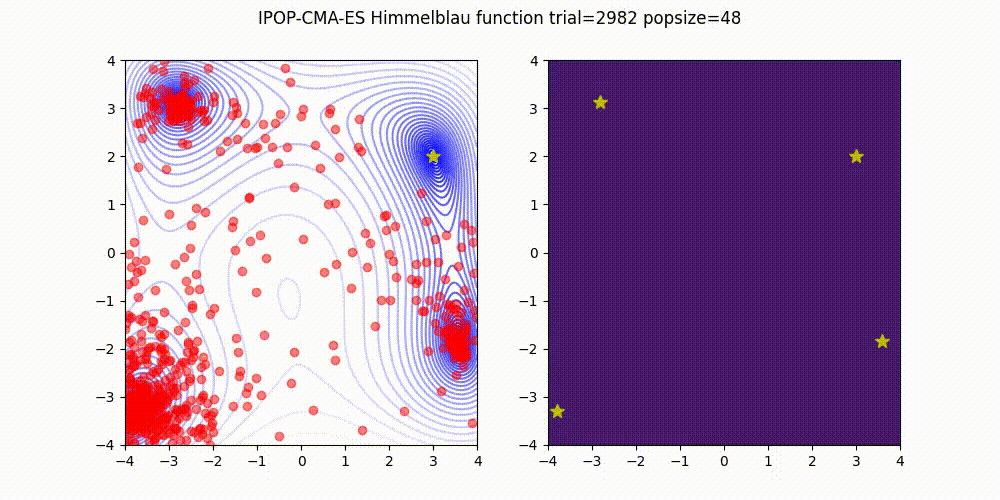
IPOP-CMA-ES [Auger and Hansen 2005]
IPOP-CMA-ES 是一种方法,它通过以下方式重启 CMA-ES:随着种群规模的逐渐增加。
源代码
import math
import numpy as np
from cmaes import CMA
def ackley(x1, x2):
# https://www.sfu.ca/~ssurjano/ackley.html
return (
-20 * math.exp(-0.2 * math.sqrt(0.5 * (x1 ** 2 + x2 ** 2)))
- math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
+ math.e + 20
)
if __name__ == "__main__":
bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
sigma = 32.768 * 2 / 5 # 1/5 of the domain width
optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ackley(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
if optimizer.should_stop():
# popsize multiplied by 2 (or 3) before each restart.
popsize = optimizer.population_size * 2
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(mean=mean, sigma=sigma, population_size=popsize)
print(f"Restart CMA-ES with popsize={popsize}")
完整的源代码可在此处找到。
引用
如果您在您的作品中使用了我们的库,请引用我们的论文
Masahiro Nomura, Masashi Shibata。
cmaes:一个简单实用的 CMA-ES Python 库
https://arxiv.org/abs/2402.01373
Bibtex
@article{nomura2024cmaes,
title={cmaes : A Simple yet Practical Python Library for CMA-ES},
author={Nomura, Masahiro and Shibata, Masashi},
journal={arXiv preprint arXiv:2402.01373},
year={2024}
}
联系方式
如有任何问题,请随时提出问题或通过nomura_masahiro@cyberagent.co.jp联系我。
链接
使用 cmaes 的项目
- Optuna:一个超参数优化框架,它使用此库作为底层支持 CMA-ES。
- Kubeflow/Katib:基于 Kubernetes 的超参数调整和神经网络架构搜索系统
- (如果您在项目中使用
cmaes并希望将其列出在此处,请提交一个GitHub问题。)
其他库
我们对所有参与CMA-ES的库都表示极大的尊重。
- pycma:最著名的CMA-ES实现,由Nikolaus Hansen创建和维护。
- pymoo:一个用于Python的多目标优化库。
- evojax:evojax为此库提供JAX端口。
- evosax:evosax提供了基于JAX的CMA-ES和sep-CMA-ES实现,灵感来源于此库。
参考文献
- [Akiba等人2019] T. Akiba, S. Sano, T. Yanase, T. Ohta, M. Koyama, Optuna: A Next-generation Hyperparameter Optimization Framework, KDD, 2019.
- [Auger和Hansen 2005] A. Auger, N. Hansen, A Restart CMA Evolution Strategy with Increasing Population Size, CEC, 2005.
- [Hamano等人2022] R. Hamano, S. Saito, M. Nomura, S. Shirakawa, CMA-ES with Margin: Lower-Bounding Marginal Probability for Mixed-Integer Black-Box Optimization, GECCO, 2022.
- [Hamano等人2024] R. Hamano, S. Saito, M. Nomura, K. Uchida, S. Shirakawa, CatCMA : Stochastic Optimization for Mixed-Category Problems, GECCO, 2024.
- [Hansen 2016] N. Hansen, The CMA Evolution Strategy: A Tutorial. arXiv:1604.00772, 2016.
- [Nomura等人2021] M. Nomura, S. Watanabe, Y. Akimoto, Y. Ozaki, M. Onishi, Warm Starting CMA-ES for Hyperparameter Optimization, AAAI, 2021.
- [Nomura等人2023] M. Nomura, Y. Akimoto, I. Ono, CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?, GECCO, 2023.
- [Nomura和Shibata 2024] M. Nomura, M. Shibata, cmaes : A Simple yet Practical Python Library for CMA-ES, arXiv:2402.01373, 2024.
- [Ros和Hansen 2008] R. Ros, N. Hansen, A Simple Modification in CMA-ES Achieving Linear Time and Space Complexity, PPSN, 2008.
项目详情
下载文件
下载适用于您的平台的文件。如果您不确定选择哪个,请了解有关安装包的更多信息。