Langevin积分器,用于具有常漂移和扩散的SDE,在具有圆形边界条件的连续区间上。
项目描述
CILES:连续区间朗吉万方程模拟器
Langevin积分器,用于具有常漂移和扩散的SDE,在具有圆形边界条件的连续区间上。
CILES是用Cython编写的,并使用GSL对漂移和扩散场进行插值,以模拟连续变量。
描述
给定一个离散的漂移场A(x)和一个(位置相关的)扩散系数B(x),此工具执行简单的SDE时间正向积分
dx(t)/dt = A(x(t)) + sqrt(B(x(t))) * eta(t)
其中eta(t)是一个高斯白噪声项,x是一个具有圆形边界(通常是0 <= x < 2PI)的区间上的变量。
漂移场A和扩散B都需要是相同维度的数组。它们内部使用gsl_interp_cspline_periodic进行插值,以提供连续的场,然后用于正向积分。
正向积分使用Euler-Murayama方案执行:x(t+dt) = x(t) + dt * A(x(t)) + r * sqrt(dt * B(x(t))),其中r是一个具有零均值和单位方差的正态分布随机数。
依赖关系
Numpy
Cython
安装
克隆仓库
python setup.py install
测试(使用nosetests):nosetests
示例用法
from ciles.integrator import LangevinIntegrator as LI
import numpy as np
drift = np.zeros(100) # no drift field
diff = np.ones(100) # constant diffusion with 1 deg^2/s
dt = 1e-3 # 1 ms timestep
tmax = 1. # simulate until 1s
# initialize the integrator
li = LI(drift, diff, dt=dt, tmax=tmax)
# simulate a single trajectory
li.run()
out = li.out更多示例
以下是来自ciles.examples的当前可用示例的绘图结果。
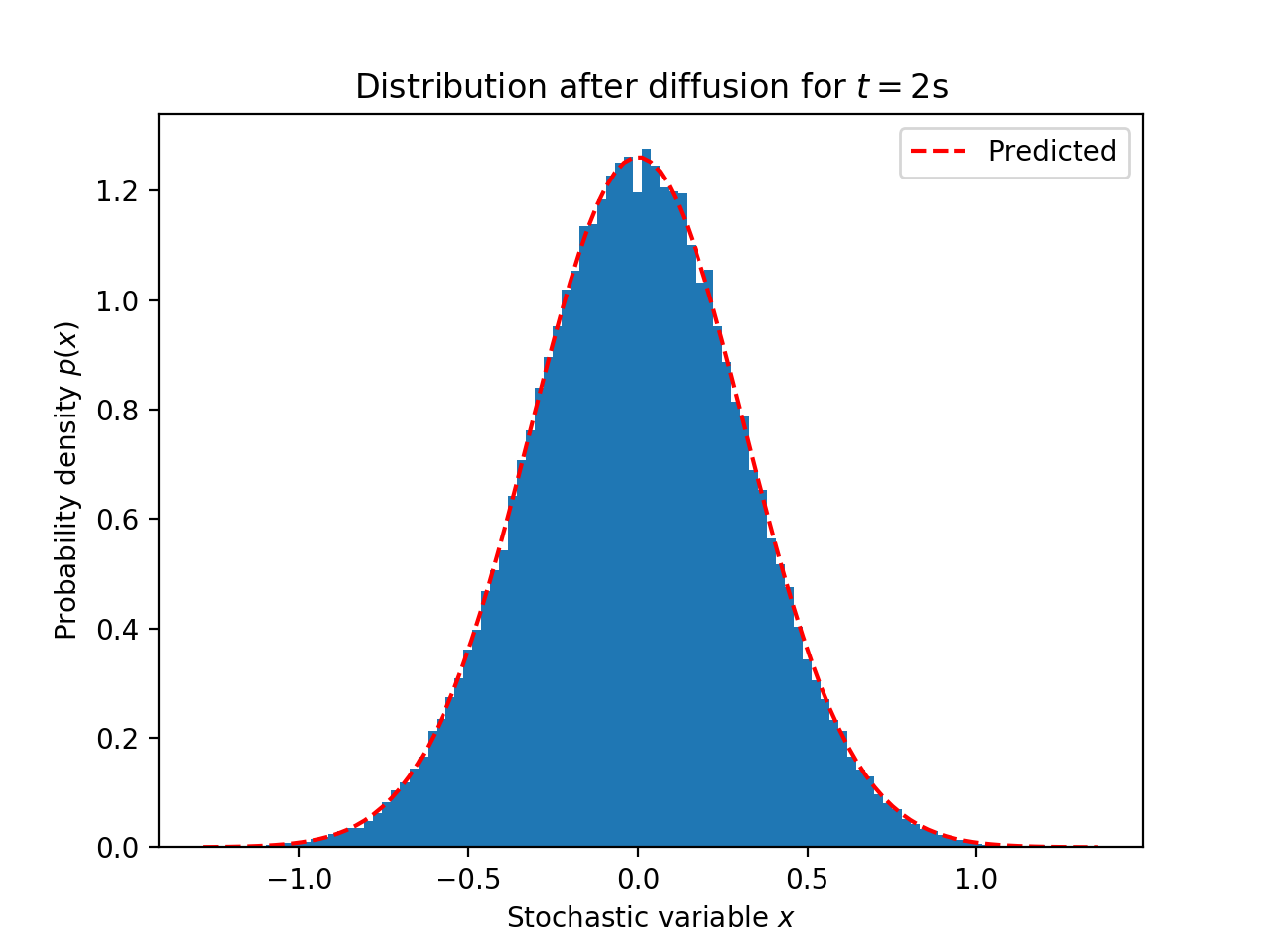
2秒扩散后的最终分布
查看源代码
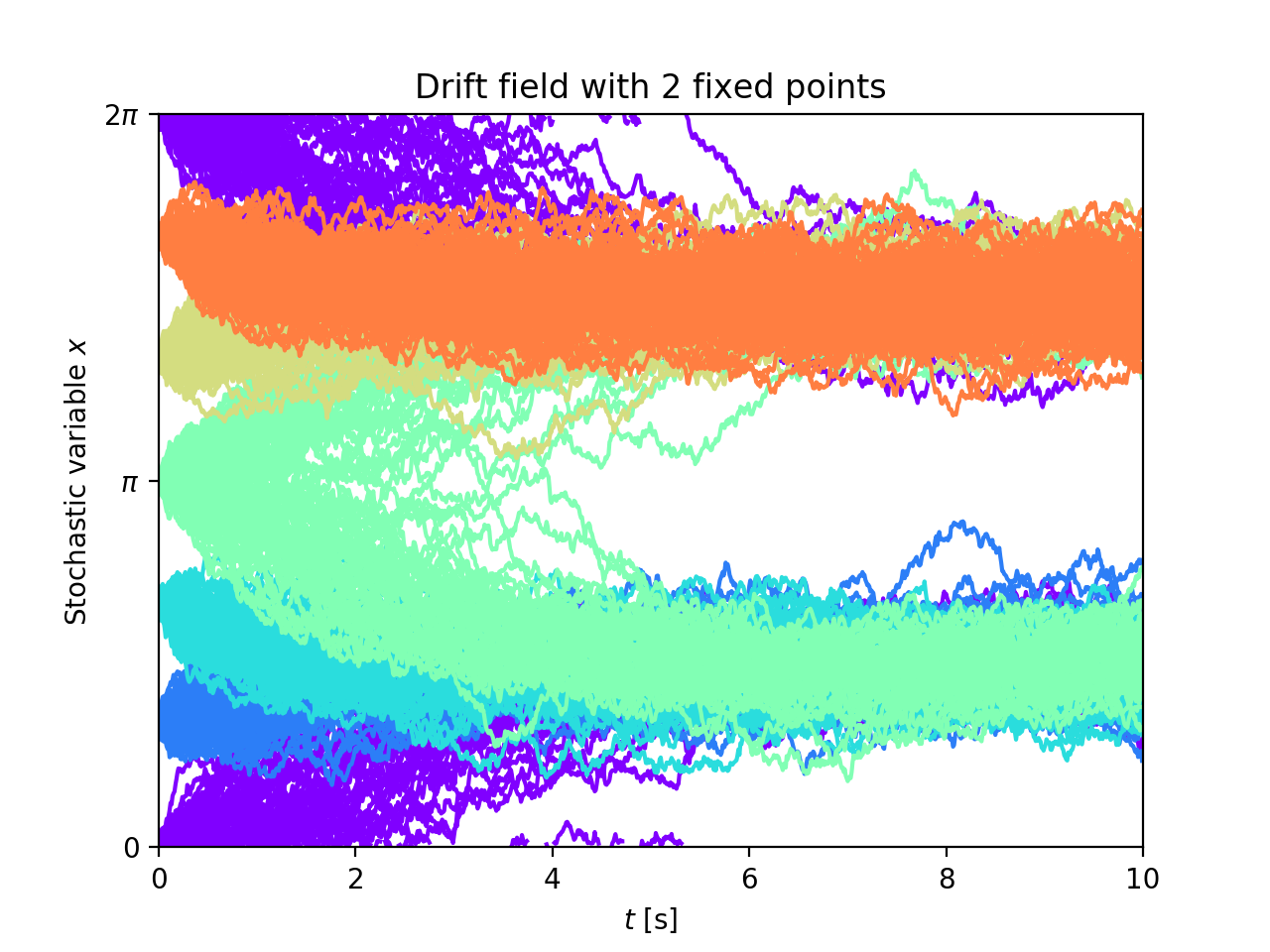
具有2个固定点的漂移场轨迹
查看源代码
项目详情
关闭
ciles-0.1.0.tar.gz的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | f9a8eb5749285cec0542ac083d6331163f05e48138d20bf33f111e216eb58d31 |
|
| MD5 | dadfae809b0476a272ebc2736ef1380e |
|
| BLAKE2b-256 | 4e32b95462360f49519064f6487f9e9fff9c99461208402b862c04a6e63449aa |
关闭
ciles-0.1.0-cp27-cp27m-macosx_10_11_x86_64.whl的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 6f762e9f76762bf003278b2ff24825bfe239d2667a14a9c20278752229b3247b |
|
| MD5 | e540ce430d9b7bf8752542c1d81d549b |
|
| BLAKE2b-256 | 353d7970983bdc4acf325458114d8c7345b4364ebf8741d134a0bf5427029dcc |