Python中的准实验因果推断
项目描述
CausalPy
CausalPy是一个专注于准实验环境中因果推断的Python包。该包允许使用传统的OLS之外,还使用复杂的贝叶斯模型拟合方法。
安装
获取最新版本
pip install CausalPy
如果您想安装包的最新版本,也可以从GitHub安装
pip install git+https://github.com/pymc-labs/CausalPy.git
快速入门
import causalpy as cp
import matplotlib.pyplot as plt
# Import and process data
df = (
cp.load_data("drinking")
.rename(columns={"agecell": "age"})
.assign(treated=lambda df_: df_.age > 21)
)
# Run the analysis
result = cp.RegressionDiscontinuity(
df,
formula="all ~ 1 + age + treated",
running_variable_name="age",
model=cp.pymc_models.LinearRegression(),
treatment_threshold=21,
)
# Visualize outputs
fig, ax = result.plot();
# Get a results summary
result.summary()
plt.show()
路线图
仓库的计划可以在问题中查看。
视频
点击下面的缩略图观看CausalPy在YouTube上的视频。
包功能概述
合成控制
当您有多个单位,其中一个被处理时,这很合适。您通过构建未处理单位的加权组合来构建一个合成控制。
| 时间 | 结果 | 控制1 | 控制2 | 控制3 |
|---|---|---|---|---|
| 0 | $y_0$ | $x_{1,0}$ | $x_{2,0}$ | $x_{3,0}$ |
| 1 | $y_1$ | $x_{1,1}$ | $x_{2,1}$ | $x_{3,1}$ |
| $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
| T | $y_T$ | $x_{1,T}$ | $x_{2,T}$ | $x_{3,T}$ |
| 频率统计 | 贝叶斯 |
|---|---|
 |
 |
数据(处理和未处理单位)、预处理模型拟合和反事实(即合成控制)被绘制(顶部)。因果关系用蓝色阴影区域表示。贝叶斯分析显示了模型拟合和反事实的贝叶斯可信区间。同时显示了因果关系(中间)和累积因果关系(底部)。
地理提升(Geolift)
我们还可以使用合成控制方法来分析地理提升研究的数据。例如,我们可以通过使用与干预区域相似但未接受特定营销干预的控制地理区域来尝试评估在一个地理区域内运行的干预措施(例如营销活动)的因果关系。
ANCOVA
当您有一个单一的前后干预测量,并且有一个治疗组和对照组时,这适用于非等价组设计。
| 组 | 前 | 后 |
|---|---|---|
| 0 | $x_1$ | $y_1$ |
| 0 | $x_2$ | $y_2$ |
| 1 | $x_3$ | $y_3$ |
| 1 | $x_4$ | $y_4$ |
| 频率统计 | 贝叶斯 |
|---|---|
| 即将推出 |  |
控制组和处理组的数据被绘制,包括后验预测的94%可信区间。下面板显示了估计的治疗效果。
双重差分法
当您有前后干预测量,并且有一个治疗组和对照组时,这适用于非等价组设计。与ANCOVA方法不同,双重差分法在存在多个前后治疗测量时是合适的。
数据应具有以下形式。这里只显示了两个单位 - 一个在处理组(group=1)和一个在未处理组(group=0),但当然每个组可以有多个单位。这是面板数据(也称为重复测量),其中每个单位在两个时间点进行测量。
| 单位 | 时间 | 组 | 结果 |
|---|---|---|---|
| 0 | 0 | 0 | $y_{0,0}$ |
| 0 | 1 | 0 | $y_{0,0}$ |
| 1 | 0 | 1 | $y_{1,0}$ |
| 1 | 1 | 1 | $y_{1,1}$ |
| 频率统计 | 贝叶斯 |
|---|---|
 |
 |
数据、模型拟合和反事实被绘制。频率统计模型拟合产生点估计,但贝叶斯分析产生后验分布,由小提琴图表示。因果关系是反事实预测(处理组,治疗后)与治疗后处理组观察值之间的差异。
回归断点设计
回归断点设计在根据运行变量的截断(例如$x$)应用治疗时使用,这通常不是时间。通过寻找在治疗截断的精确点处的断点存在,我们可以就治疗的潜在影响做出因果关系声明。
| 运行变量 | 结果 | 处理 |
|---|---|---|
| $x_0$ | $y_0$ | 假 |
| $x_1$ | $y_0$ | 假 |
| $\ldots$ | $\ldots$ | $\ldots$ |
| $x_{N-1}$ | $y_{N-1}$ | 真 |
| $x_N$ | $y_N$ | 真 |
| 频率统计 | 贝叶斯 |
|---|---|
 |
 |
数据、模型拟合和反事实被绘制(顶部)。频率统计分析用蓝色阴影区域显示因果关系,但在贝叶斯分析中未显示,以避免图表杂乱。相反,贝叶斯分析显示了模型拟合的贝叶斯可信区间。频率统计分析可视化因果影响的点估计,但贝叶斯分析还绘制了回归断点效应的后验分布(底部)。
回归扭曲设计
回归间断性设计用于处理根据连续变量的截断值对单位进行处理的情境,其中截断值通常不是时间。通过在处理截断的精确点寻找不连续性,我们可以就治疗的潜在影响做出因果推断。
| 运行变量 | 结果 |
|---|---|
| $x_0$ | $y_0$ |
| $x_1$ | $y_0$ |
| $\ldots$ | $\ldots$ |
| $x_{N-1}$ | $y_{N-1}$ |
| $x_N$ | $y_N$ |
| 频率统计 | 贝叶斯 |
|---|---|
| 即将推出 |  |
数据和模型拟合。贝叶斯分析显示了后验均值和置信区间(阴影区域)。我们还报告了数据上的贝叶斯 $R^2$,以及梯度变化在拐点处的后验均值和置信区间。
中断时间序列
当您有一组在特定时间点接受处理的观测时间序列时,中断时间序列分析是合适的。这种分析没有对照组,而是在处理时间或之后寻找结果测量的变化。可以包括多个预测变量。
| 时间 | 结果 | 处理 | 预测变量 |
|---|---|---|---|
| $t_0$ | $y_0$ | 假 | $x_0$ |
| $t_1$ | $y_0$ | 假 | $x_1$ |
| $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
| $t_{N-1}$ | $y_{N-1}$ | 真 | $x_{N-1}$ |
| $t_N$ | $y_N$ | 真 | $x_N$ |
| 频率统计 | 贝叶斯 |
|---|---|
 |
 |
数据、预处理模型拟合和反事实被绘制(顶部)。因果关系以蓝色阴影区域表示。贝叶斯分析显示了模型拟合和反事实的贝叶斯置信区域。还包括因果关系(中间)和累积因果关系(底部)。
工具变量回归
当您希望估计一个变量的处理效应对另一个变量的影响,但担心处理变量在感兴趣的系统内是内生的(即与误差相关)时,工具变量回归是一种合适的技巧。在这种情况下,可以在回归中使用“工具”变量来解开由内生性引起的混杂威胁所导致的处理效应。
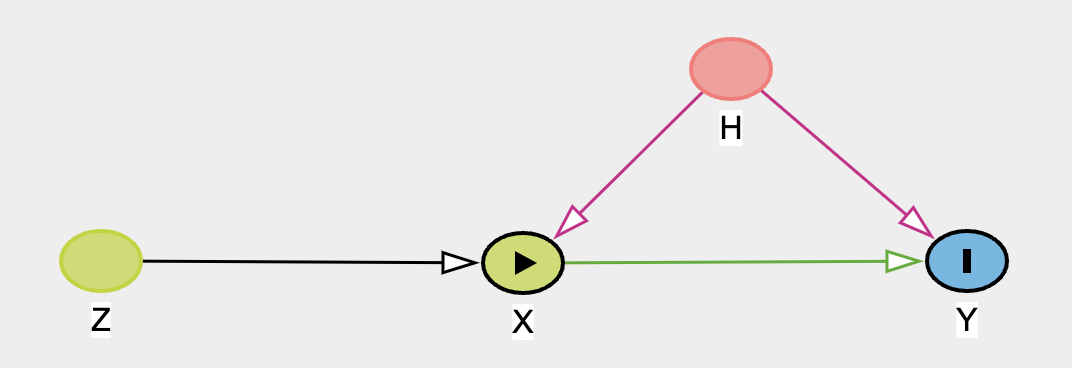
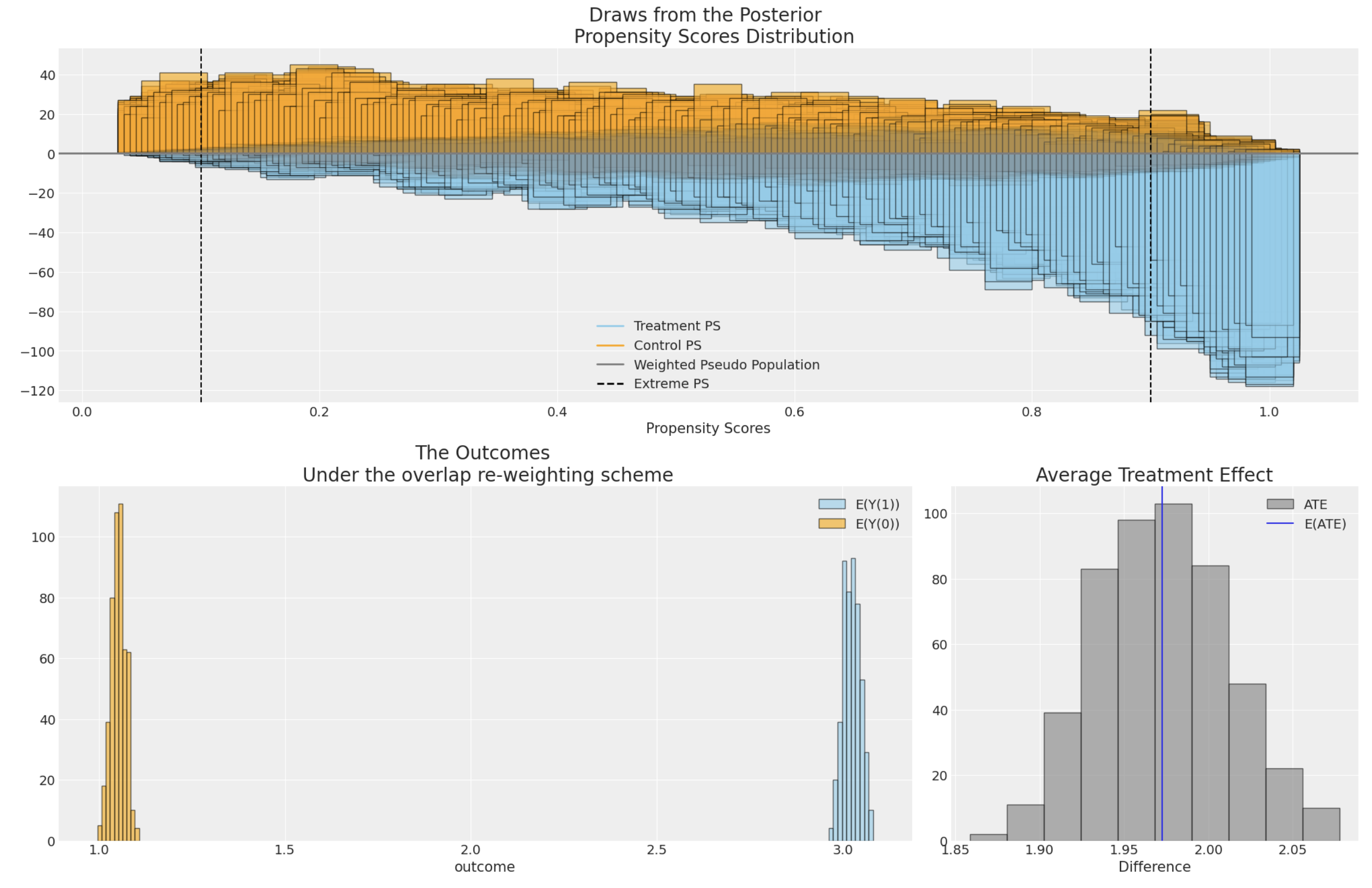
逆倾向得分加权
倾向得分通常用于解决观察性研究中由选择效应引入的治疗条件中的偏差或混杂风险。倾向得分可以以多种方式使用,但在这里我们展示了它们在旨在恢复治疗条件下按随机分配的受试者的校正加权方案中的使用。该技术“增加”或“减少”单个观测值的权重,以更好地估计因果估计量,如平均处理效应。
学习资源
以下是一些关于因果推断的一般资源
- 官方PyMC示例画廊有一系列与因果推断特别相关的示例。
- Angrist, J. D. 和 Pischke, J. S. (2009). 无害的计量经济学:经验主义者的伴侣。普林斯顿大学出版社。
- Angrist, J. D. 和 Pischke, J. S. (2014). 掌握计量经济学:从原因到效果的道路。普林斯顿大学出版社。
- Cunningham, S. (2021). 因果推断:The Mixtape。耶鲁大学出版社。
- Huntington-Klein, N. (2021). 效果:研究设计和因果性的介绍。Chapman and Hall/CRC。
- Reichardt, C. S. (2019). 类实验:设计和分析的指南。Guilford Publications。
许可证
支持

此存储库由PyMC Labs支持。
如果您想了解PyMC Labs能为您做什么,请发送电子邮件至ben.vincent@pymc-labs.com。我们与各种规模的公司合作,并与不同水平的现有建模能力合作。我们还运行企业研讨会培训活动,并提供从贝叶斯入门到更高级主题的会话。
项目详情
下载文件
下载适合您平台文件的文件。如果您不确定选择哪个,请了解更多关于安装包的信息。