工作记忆实验的混合模型
项目描述
有偏记忆工具箱
一个用于视觉工作记忆实验数据混合模型的Python工具箱
Cherie Zhou (@cherieai) 和 Sebastiaan Mathôt (@smathot)
版权 2020 - 2022
内容
引用
Zhou, C., Lorist, M., Mathôt, S., (2021). 视觉工作记忆中的分类偏差:记忆负载和保持间隔的影响。 Cortex. https://osf.io/puq4v/
这篇手稿是已注册报告的第一阶段原则性接受
安装
pip install biased_memory_toolbox
使用
本节重点介绍模块的使用,假设您已经对工作记忆数据混合模型有基本了解。如果您想了解更多关于混合模型背后的理论,请阅读(例如)上述引用的手稿。
我们首先使用DataMatrix读取数据文件。数据应包含一个包含备忘录(此处:memory_hue)的列和一个包含响应(此处:response_hue)的列,两者都在0到360度之间。
from datamatrix import io
dm = io.readtxt('example-data/example-participant.csv')
作为第一步,这与混合模型本身无关,我们检查参与者是否显著(p < .05)超过机会水平。这是通过实现为test_chance_performance()的置换检验来完成的。在这里,低p值表示表现偏离了机会。
import biased_memory_toolbox as bmt
t, p = bmt.test_chance_performance(dm.memory_hue, dm.response_hue)
print('testing performance: t = {:.4f}, p = {:.4f}'.format(t, p))
输出
testing performance: t = -56.7786, p = 0.0000
现在我们来拟合混合模型。我们从一个仅估计精度和猜测率的基模型开始,就像在原始Zhang and Luck (2008)论文中一样。
为此,我们首先计算响应误差,这实际上是记忆色(参与者需要记住的颜色)与响应色(参与者再现的颜色)之间的环形距离。这通过response_bias()函数实现,当不提供类别时,它仅计算响应误差。
dm.response_error = bmt.response_bias(dm.memory_hue, dm.response_hue)
我们可以通过简单调用fix_mixture_model()来拟合模型。通过指定include_bias=False,我们将偏差参数(分布的均值)固定在0,因此只得到两个参数:精确度和猜测率。
precision, guess_rate = bmt.fit_mixture_model(
dm.response_error,
include_bias=False
)
print('precision: {:.4f}, guess rate: {:.4f}'.format(precision, guess_rate))
输出
precision: 1721.6386, guess rate: 0.0627
现在让我们拟合一个稍微复杂一些的模型,该模型还包括一个偏差参数。要这样做,我们首先计算响应'偏差',它类似于响应误差,但编码方式不同,使得正值表示对所属类别原型的响应误差。例如,如果参与者看到略带绿色的水绿色,但再现的是纯绿色,那么这将对该响应产生正响应偏差。
为了计算响应偏差,我们需要在调用response_bias()时指定一个包含类别边界和原型的dict。工具箱提供了一个合理的默认值(DEFAULT_CATEGORIES),该值基于Zhou, Mathôt, & Lorist, 2021b的人参与者评分。另一个评分集,来自Zhou, Mathôt, & Lorist, 2021a,作为CORTEX_CATEGORIES提供。
dm.response_bias = bmt.response_bias(
dm.memory_hue,
dm.response_hue,
categories=bmt.DEFAULT_CATEGORIES
)
接下来,我们再次通过调用fit_mixture_model()来拟合模型。我们现在还得到了一个偏差参数(因为我们没有指定include_bias=False),如Zhou, Lorist, and Mathôt (2021)所述。
precision, guess_rate, bias = bmt.fit_mixture_model(dm.response_bias)
print(
'precision: {:.4f}, guess rate: {:.4f}, bias: {:.4f}'.format(
precision,
guess_rate,
bias
)
)
输出
precision: 1725.9568, guess rate: 0.0626, bias: 0.5481
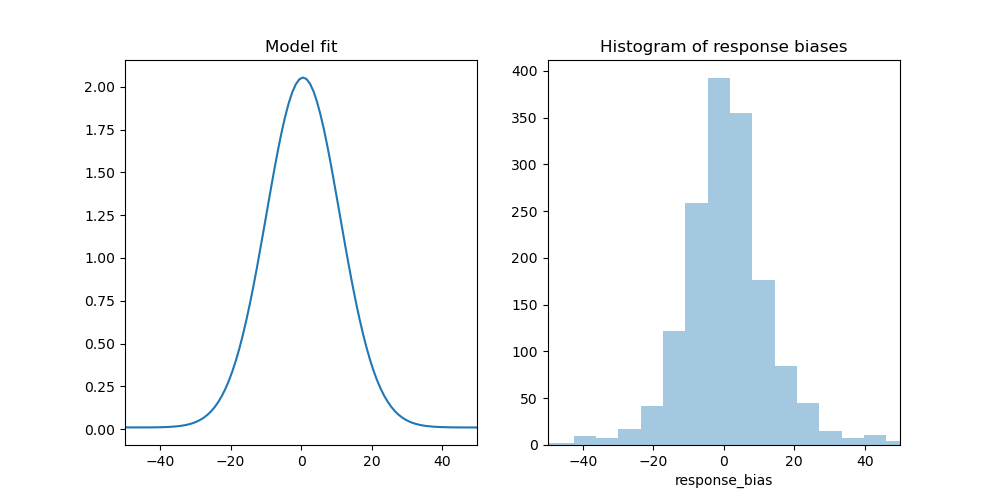
可视化模型拟合也是有意义的,以查看模型是否准确地捕捉了响应模式。我们可以通过绘制概率密度函数来实现,该函数可以通过mixture_model_pdf()生成。
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
x = np.linspace(-180, 180, 360)
y = bmt.mixture_model_pdf(x, precision, guess_rate, bias)
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.title('Model fit')
plt.xlim(-50, 50)
plt.plot(x, y)
plt.subplot(122)
plt.title('Histogram of response biases')
plt.xlim(-50, 50)
sns.distplot(dm.response_bias, kde=False)
plt.savefig('example.png')
我们还可以拟合一个考虑交换错误的模型,如Bays, Catalao, and Husain (2009)所述。为此,我们还需要指定相对于非目标项的响应偏差(或普通误差)。
在这里,我们只选择那些集大小为3的试验,然后为第二个和第三个记忆颜色(在这个实验中是非目标)创建两个新的响应偏差列。(第一个颜色是目标颜色。)
dm3 = dm.set_size == 3
dm3.response_bias_nontarget2 = bmt.response_bias(
dm3.hue2,
dm3.response_hue,
categories=bmt.DEFAULT_CATEGORIES
)
dm3.response_bias_nontarget3 = bmt.response_bias(
dm3.hue3,
dm3.response_hue,
categories=bmt.DEFAULT_CATEGORIES
)
通过传递非目标响应偏差的列表,我们得到第四个参数:交换率。
precision, guess_rate, bias, swap_rate = bmt.fit_mixture_model(
x=dm3.response_bias,
x_nontargets=[
dm3.response_bias_nontarget2,
dm3.response_bias_nontarget3
],
)
print(
'precision: {:.4f}, guess rate: {:.4f}, bias: {:.4f}, swap_rate: {:.4f}'.format(
precision,
guess_rate,
bias,
swap_rate
)
)
输出
precision: 1458.9628, guess rate: 0.0502, bias: 1.2271, swap_rate: 0.0191
函数参考
biased_memory_toolbox.category(x, categories)
获取x所属的类别。例如,如果x对应于略带橙色的红色,则类别将是'red'。
参数
- x: float or int : 以度为单位(0 - 360)的值
- categories: dict : 参见reponse_bias()
返回
str 一个类别标签
biased_memory_toolbox.fit_mixture_model(x, x_nontargets=None, include_bias=True, x0=None, bounds=None)
将偏差混合模型拟合到数据集中。混合模型的输入通常是由响应偏差组成,当拟合偏差参数时,由response_bias()确定,或者当未拟合偏差参数时,由有符号的响应误差组成。
参数
- x: array_like : 一个数组,DataMatrix列,或其他可迭代对象,表示响应偏差
- x_nontargets: list, optional : 一个数组列表,DataMatrix列,或其他可迭代对象,表示相对于非目标的响应偏差。如果提供了此参数,则返回一个交换率作为最终参数。
- include_bias: bool, optional : 指示是否拟合偏差参数。
- x0: list, optional : 参数的起始值列表。顺序:精确度,猜测率,偏差。如果没有为参数提供起始值,则将其保留为
mixture_model_pdf()的默认值。 - bounds:列表,可选:参数的上限和下限元组的列表。如果没有提供值,则使用默认值。
返回
元组 参数的元组。根据参数,这些是以下之一
- (precision, guess rate)
- (precision, guess rate, bias)
- (precision, guess rate, swap rate)
- (precision, guess rate, bias, swap rate)
biased_memory_toolbox.mixture_model_pdf(x, precision=500, guess_rate=0.1, bias=0)
返回混合模型的概率密度函数。
参数
- x:array_like:x轴值的列表(或其他可迭代对象)。例如
range(-180, 181)将为每个相关值生成PDF。 - precision:float,可选:精度(或kappa)参数。这与标准差成反比,是一个度数值。
- guess_rate:float,可选:猜测响应的比例(0 - 1)。
- bias:float,可选:度数偏差(或loc)参数。
返回
数组 包含每个x值概率密度的数组。
biased_memory_toolbox.prototype(x, categories)
获取x所属类别的原型。例如,如果x对应于略带橙色的红色,则原型将是典型红色色调。
参数
- x: float or int : 以度为单位(0 - 360)的值
- categories: dict : 参见reponse_bias()
返回
float或int 度数(0-360)的原型值。
biased_memory_toolbox.response_bias(memoranda, responses, categories=None)
计算响应偏差,即响应与记忆之间的误差,该误差与记忆所属类别的原型方向一致。例如,如果记忆是一个略带橙色的红色,则正值表示向典型红色方向的误差,而负值表示向黄色类别的误差。
参数
-
memoranda:array_like:包含度数(0-360)值数组的数组、DataMatrix列或其他可迭代对象。
-
responses:array_like:包含度数(0-360)值数组的数组、DataMatrix列或其他可迭代对象。
-
categories:dict,可选:定义类别的字典。键是类别的名称,值是表示类别开始和结束位置以及典型值的(start_value, end_value, prototype)值。
请参阅
biased_memory_toolbox.DEFAULT_CATEGORIES和biased_memory_toolbox.CORTEX_CATEGORIES,了解两套类别评分。
返回
列表 响应偏差值的列表。
biased_memory_toolbox.test_chance_performance(memoranda, responses)
测试响应是否高于偶然水平。这是通过首先确定实际误差和记忆,然后确定记忆和随机响应之间的随机误差来完成的。最后,进行独立t检验以比较实际和随机误差。由于随机化,确切值会有所不同。
参数
- memoranda:array_like:包含度数(0-360)值数组的数组、DataMatrix列或其他可迭代对象。
- responses:array_like:包含度数(0-360)值数组的数组、DataMatrix列或其他可迭代对象。
返回
元组 (t_value, p_value) 元组。
许可
biased_memory_toolbox 在 GNU通用公共许可证v3 下授权。
项目详细信息
下载文件
下载适合您的平台的文件。如果您不确定选择哪个,请了解有关 安装包 的更多信息。
源分发
构建发行版
biased_memory_toolbox-1.3.0.tar.gz 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 19fe3bd4c914ce6e1cf3350d951d42fb654016360ceadc2b5618640c12f9c7ab |
|
| MD5 | c2d40313ec6f3bc27467e586a42b2393 |
|
| BLAKE2b-256 | d99bcfe1a1e4178052423853b9944a8678e05bdf388a15e513091edb2049fa2d |
biased_memory_toolbox-1.3.0-py3-none-any.whl 的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | ccc399915d7e8d97c768c21a71ac9ae927caf7b1a36d448ea0c0521ddbe9a3dc |
|
| MD5 | 2df69b4152ddd41f29728ed1f354cea6 |
|
| BLAKE2b-256 | 676b2a41afa22f12e8b4af320103cb3486c80477d514ffcf970ea17eaea70b51 |