Python的自动微分
项目描述
ADiPy是一个快速、纯Python自动微分(AD)库。此软件包提供以下功能
任意阶一元微分
一阶多元微分
一元泰勒多项式函数生成器
雅可比矩阵生成器
兼容线性代数例程
安装
要安装adipy,请在终端窗口中执行以下操作之一(可能需要管理员权限)
下载tar包,解压,然后在解压目录中运行python setup.py install。
运行easy_install [--upgrade] adipy
运行pip install [--upgrade] adipy
如何开始
首先,我们使用简单的导入
from adipy import *
这导入必要的构造函数和基本函数(sin,exp,sqrt等),以及np,它是根NumPy模块。
现在,我们可以使用ad(...)或adn(...)来构建AD对象。对于多元操作,建议使用ad(...)函数一次性构建所有对象,但这不是必需的。如果它们分别初始化,语法会稍微复杂一些。
一元示例
以下是一些一元操作的示例
# A single, first-order differentiable object x = ad(1.5) y = x**2 print y # output is: ad(2.25, array([3.0])) # What is dy/dx? print y.d(1) # output is: 3.0 z = x*sin(x**2) print z # output is: ad(1.1671097953318819, array([-2.0487081053644052])) # What is dz/dx? print z.d(1) # output is: -2.0487081053644052 # A single, fourth-order differentiable object x = adn(1.5, 4) y = x**2 print y # output is: ad(2.25, array([ 3., 2., 0., -0.])) # What is the second derivative of y with respect to x? print y.d(2) # output is: 2.0 z = x*sin(x**2) print z # output is: # ad(1.1671097953318819, array([ -2.04870811, -16.15755076, -20.34396265, 194.11618384])) # What is the fourth derivative of z with respect to x? print z.d(4) # output is: 194.116183837
从示例中可以看出,当打印AD对象时,你会看到两组数字。第一组是名义值,或零阶导数。下一组值是1阶到N阶导数,在名义值处评估。
多元示例
对于多元会话,情况略有不同,目前只能处理一阶导数(目前是这样),但行为相似
x = ad(np.array([-1, 2.1, 0.25])) y = x**2 print y # output is: # ad(array([ 1. , 4.41 , 0.0625]), array([[[-2. , 0. , 0. ], # [-0. , 4.2, 0. ], # [-0. , 0. , 0.5]]]))
这实际上只是对每个对象执行了**2运算符,因此我们可以看到每个数组索引的导数以及它们之间是如何相互独立的。使用标准的索引操作,我们可以访问AD多元对象的单个元素
print x[0] # output is: # ad(-1, array([ 1., 0., 0.]))
如果我们想在计算中使用多个AD对象,让我们看看会发生什么
z = x[0]*sin(x[1]*x[2]) print z # output is: # ad(-0.50121300467379792, array([[ 0.501213 , -0.21633099, -1.81718028]]))
这里的结果显示了z的名义值,但也显示了每个x值的偏导数。因此,dz/dx[0] = 0.501213等。
雅可比矩阵
如果我们有多个输出,例如
y = [0]*2 y[0] = x[0]*x[1]/x[2] y[1] = -x[2]**x[0]
我们可以使用jacobian函数来总结y每个索引的偏导数
print jacobian(y) # output is: [[ 8.4 -4. 33.6 ] # [ 5.54517744 0. 16. ]]
就像之前一样,我们可以提取第一阶偏导数
print z.d(1) # output is: [ 0.501213 -0.21633099 -1.81718028]
对于y对象,我们目前还不能使用d(...)函数,因为它是技术上的一个列表。然而,我们可以使用unite函数将其转换为单个多元AD对象,然后我们将有权访问d(...)函数。在两种情况下,jacobian函数的结果是相同的
y = unite(y) print y.d(1) # output is: [[ 8.4 -4. 33.6 ] # [ 5.54517744 0. 16. ]] print jacobian(y) # output is: [[ 8.4 -4. 33.6 ] # [ 5.54517744 0. 16. ]]
就像之前提到的,多元会话可以初始化单个独立的AD对象,尽管不如以前方便,如下所示
x = ad(-1, np.array([1, 0, 0])) y = ad(2.1, np.array([0, 1, 0])) z = ad(0.25, np.array([0, 0, 1]))
这允许跟踪所有偏导数,并在初始化时记录在相应的单一索引上。与单一构建相反,如果需要,我们可以分离出单个元素
x, y, z = ad([np.array([-1, 2.1, 0.25]))
结果是一样的。
一元泰勒级数近似
对于一元函数,我们可以使用taylorfunc函数生成一个可调用的函数,允许近似到指定的阶数
x = adn(1.5, 6) # a sixth-order AD object z = x*sin(x**2) fz = taylorfunc(z, at=x.nom)
"at"关键字指定级数展开的点,这很可能是原始独立AD对象的名义值(例如,x.nom)。现在,每次需要近似x*sin(x**2)时,我们都可以使用fz,但要知道,它从x.nom评估得越远,近似中的误差就越大。
如果安装了Matplotlib,我们可以看到近似泰勒多项式的阶数的差异
import matplotlib.pyplot as plt
xAD = [adn(1.5, i) for i in xrange(1, 7)] # a list of ith-order AD objects
def z(x):
return x*sin(x**2)
x = np.linspace(0.75, 2.25)
plt.plot(x, z(x), label='Actual Function')
for i in xrange(len(xAD)):
fz = taylorfunc(z(xAD[i]), at=xAD[i].nom)
plt.plot(x, fz(x), label='Order %d Taylor'%(i+1))
plt.legend(loc=0)
plt.show()
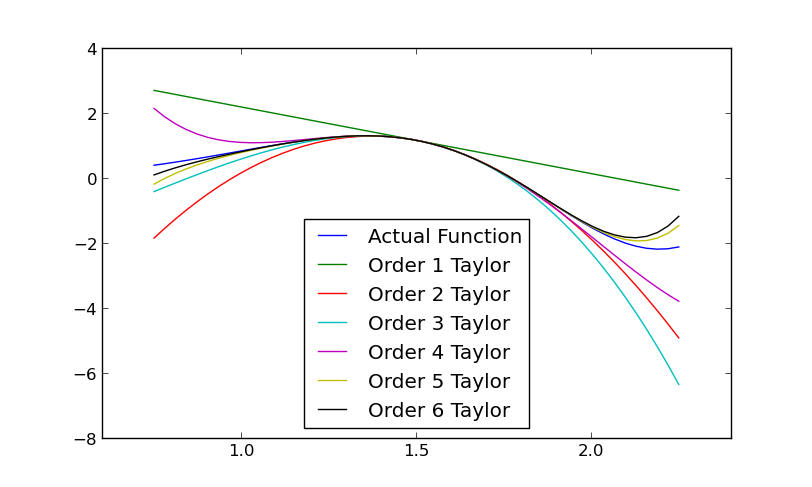
请注意,在x=1.5时,所有近似都是完美准确的(正如我们预期的那样),误差随着近似从该点远离而增加,但近似阶数的增加减少了误差。
线性代数
有几个与AD兼容的线性代数例程可用
分解
Cholesky (chol)
QR (qr)
LU (lu)
线性系统求解器
通用求解器,支持多个输出(solve)
最小二乘求解器(lstsq)
矩阵逆(inv)
矩阵范数
Frobenius范数,或2-范数(norm)
这些需要单独导入 import adipy.linalg,然后可以使用类似 adipy.linalg.solve(...) 的方式。
请参阅源代码以获取相关文档和示例。如果您熟悉NumPy版本,会发现这些很容易使用。
支持
如有任何问题、评论或关于如何使用 adipy 的良好示例,请与作者联系!
许可证
本软件包采用BSD许可证发布。它对公共和商业使用免费,并且可以免费复制,前提是给出作者适当的信用。
项目详情
ADiPy-0.6.3.tar.gz的哈希值
| 算法 | 哈希摘要 | |
|---|---|---|
| SHA256 | 192364bc95595ce97eaa788fc8d74d0f6a16fb8f0deabe494d507082cc335b97 |
|
| MD5 | 1b69d678681a0c3bba797f4a81cfe3ba |
|
| BLAKE2b-256 | 11b31ab4d7942434271be69a0e3846bc94993af93f9bb80d776fae8f85960ed0 |











